В.В. Вельтищев
8
мированное значение
/
,
K K K
=
ном
э
э э
где
K
ном
э
— предельный коэффи-
циент усиления ГП при давлении
P
н
=
P
н max
. С учетом этого получим
(
)
(
)
(
)
(
)
2
2
2
0
0
1
1
,
P
P
K
P P P P
−
−
=
−
−
ст
ст
э
н ст
н ст
(7)
где
0
0 max
max
/
;
/
.
P P P P P P
=
= ∆
н н н
ст
ст н
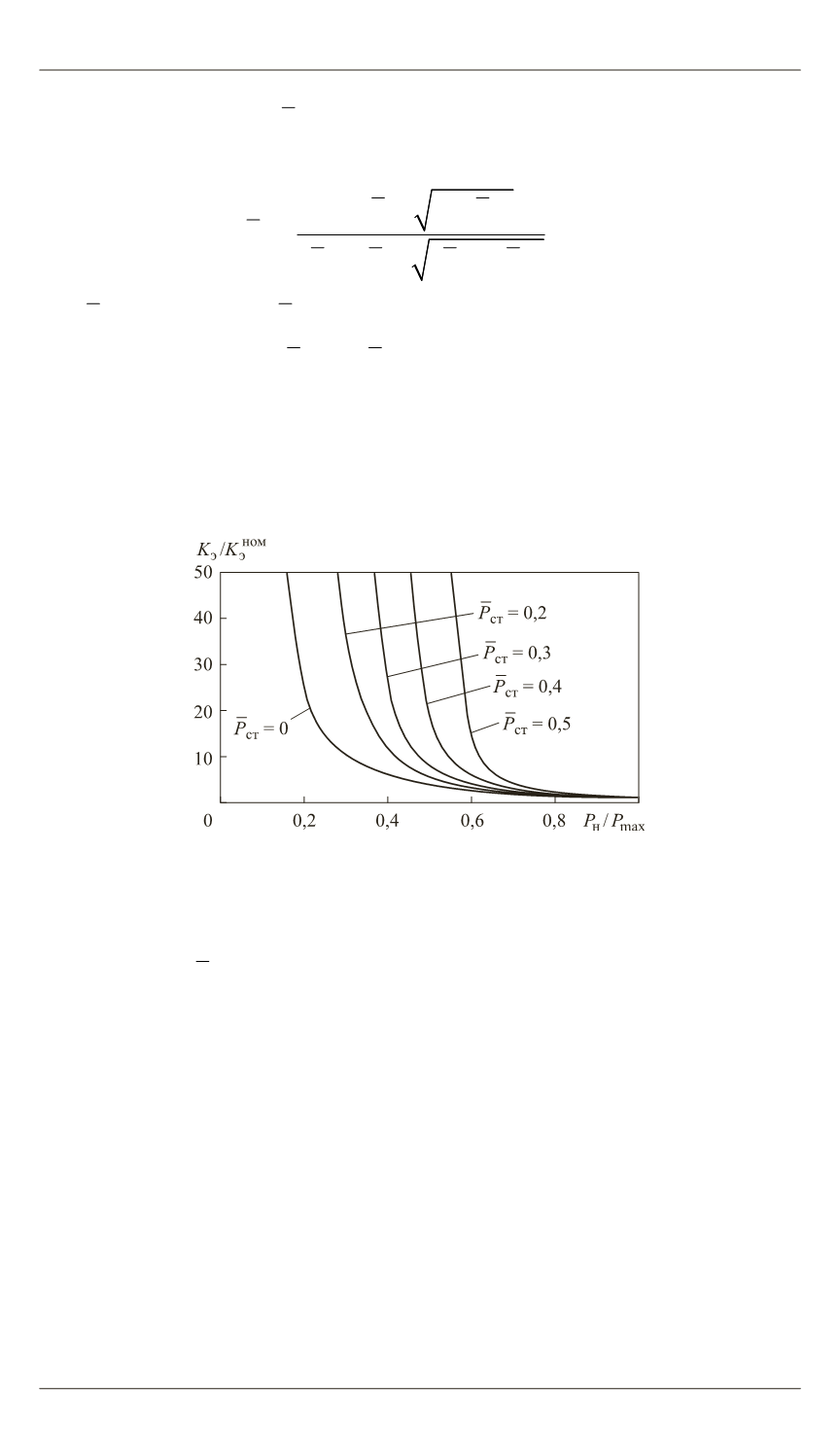
Графики функции
( )
0
K f P
=
э
н
при различных уровнях статической
нагрузки на ГП изображены на рис. 5. Вид графиков показывает, что
при уменьшении давления нагнетания на облегченных режимах работы
адаптивного к нагрузке ГП запасы устойчивости существенно возрас-
тают. Это создает условия для целенаправленного изменения коэффи-
циента
K
э
по алгоритму (8).
Рис. 5.
Зависимость граничного коэффициента усиления ГП от давления
нагнетания
На рис. 6 изображены графики изменения нормированной вели-
чины ошибки
/
ε = ε ε
ном
уст уст уст
в скорректированном ГП. Предлагаемый
алгоритм управления особенно эффективен в статически нагруженных
приводах, таких как исполнительные системы подводных манипулято-
ров. Как видно из графиков на рис. 6, точность работы адаптивного
к нагрузке ГП с использованием нелинейной коррекции коэффициента
усиления может возрастать более чем на порядок.
Реализация алгоритма самонастройки с использованием функции
(7) возможна несколькими путями. Пусть устройство регулирования
давления постоянно обеспечивает давление в гидросистеме, равное
P
н
=
P
нmin
+ Δ
P
ст
, где
P
нmin
— минимальный уровень давления, необхо-
димый для работы ГП с заданными скоростями и ускорениями на хо-
лостом ходу. Отметим, что в подводных манипуляционных устройствах
движение без груза с удовлетворительными скоростями обеспечивается
уже при
P
н min
= 5 МПа.


