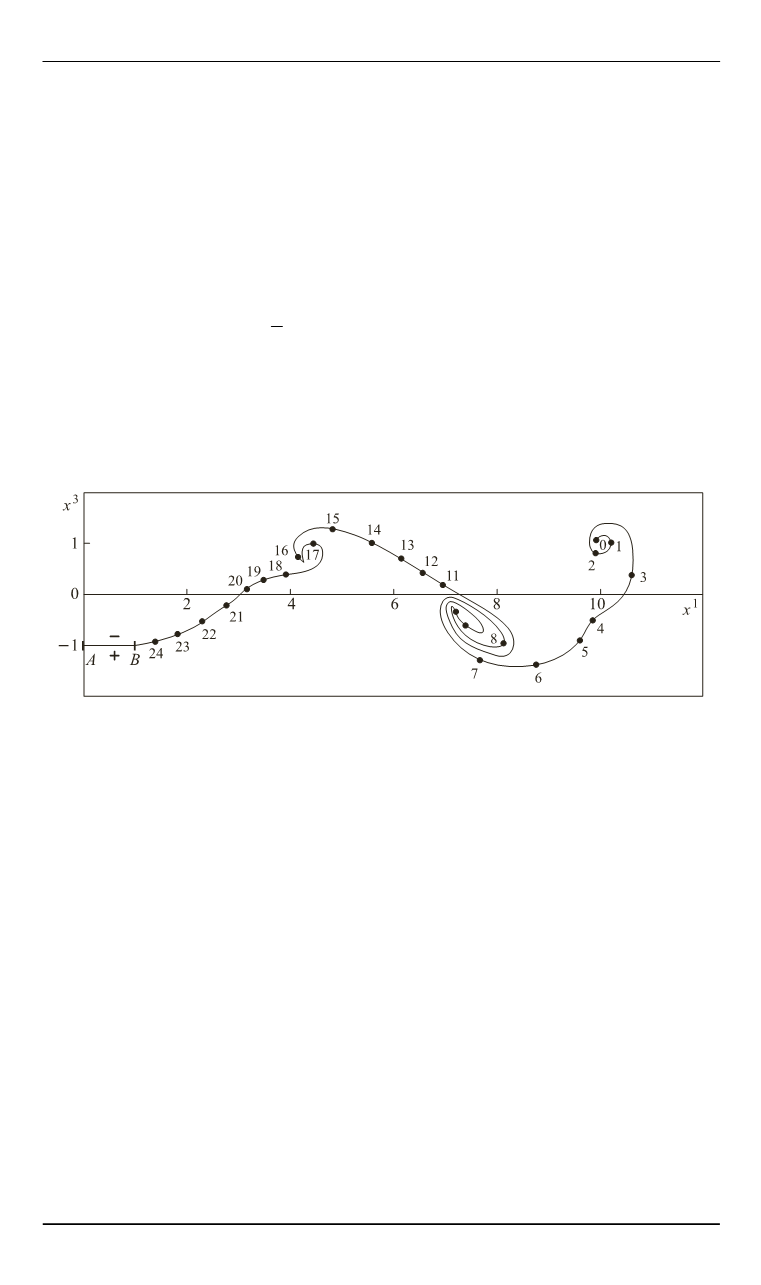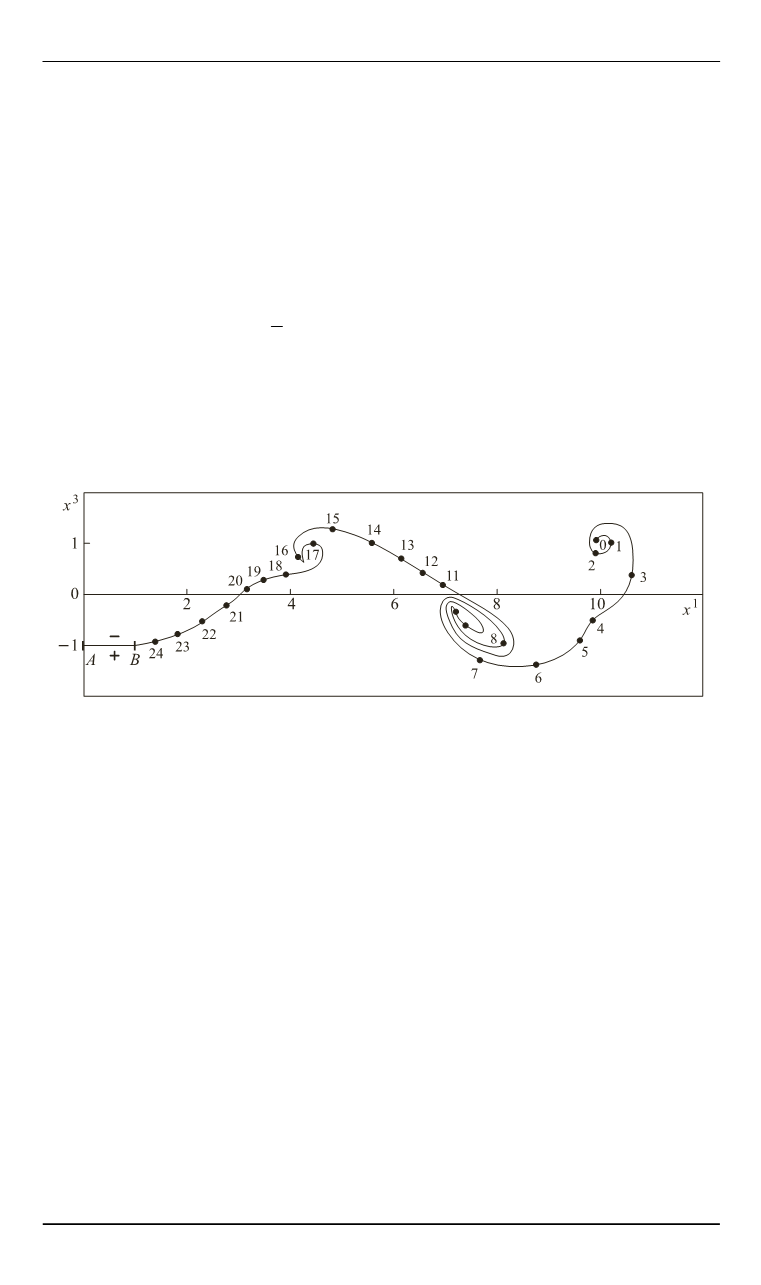
Обтекание колеблющегося крыла потоком идеальной несжимаемой жидкости
17
лом. Поскольку такое исследование усложняется трехмерностью кар-
тины обтекания, ограничимся рассмотрением свободной вихревой
поверхности в плоскости симметрии течения [14, 15]. На рис. 6 пока-
зано положение свободной вихревой поверхности в плоскости
1 3
x x
при
3
за крылом 1, закон движения которого определяется урав-
нениями (24) со следующими значениями параметров:
1,
h
0
1,
b
1.
Здесь отрезком
AB
изображена корневая хорда крыла (точка
A
соответствует кромке натекания корневой хорды), точками пока-
заны положения узловых точек (рядом с точками приведены их ла-
гранжевы координаты
1
1
b b
,
0, 1, 2, ..., ).
q
Анализ результатов
расчетов показывает, что с течением времени в плоскости
1 3
x x
сво-
бодная вихревая поверхность закручивается вокруг точек, в которых
интенсивность завихренности максимальная по абсолютному значе-
нию.
Рис. 6. Положение свободной вихревой поверхности в плоскости
1 3
x x
в момент времени
3
Заключение.
Проведенное сравнение результатов расчетов с
экспериментальными данными по кинематике плавания дельфинов
показало, что модель плавника с формой в плане, близкой к форме
хвостового плавника дельфина, удовлетворительно описывает име-
ющиеся экспериментальные данные. Совпадение результатов расче-
тов для модели прямоугольной формы с экспериментальными дан-
ными является неудовлетворительным.
Расчеты свидетельствует, что дельфины при длительном равно-
мерном движении используют наиболее рациональный гидродина-
мический механизм плавания, при котором максимально возможная
часть затрачиваемой на колебания хвостового плавника мощности
расходуется на производство полезной работы по перемещению тела
животного.
Работа выполнена при поддержке РФФИ (проект № 13-08-00538-а).