
Д.А. Маслов
10
Инженерный журнал: наука и инновации
# 10·2017
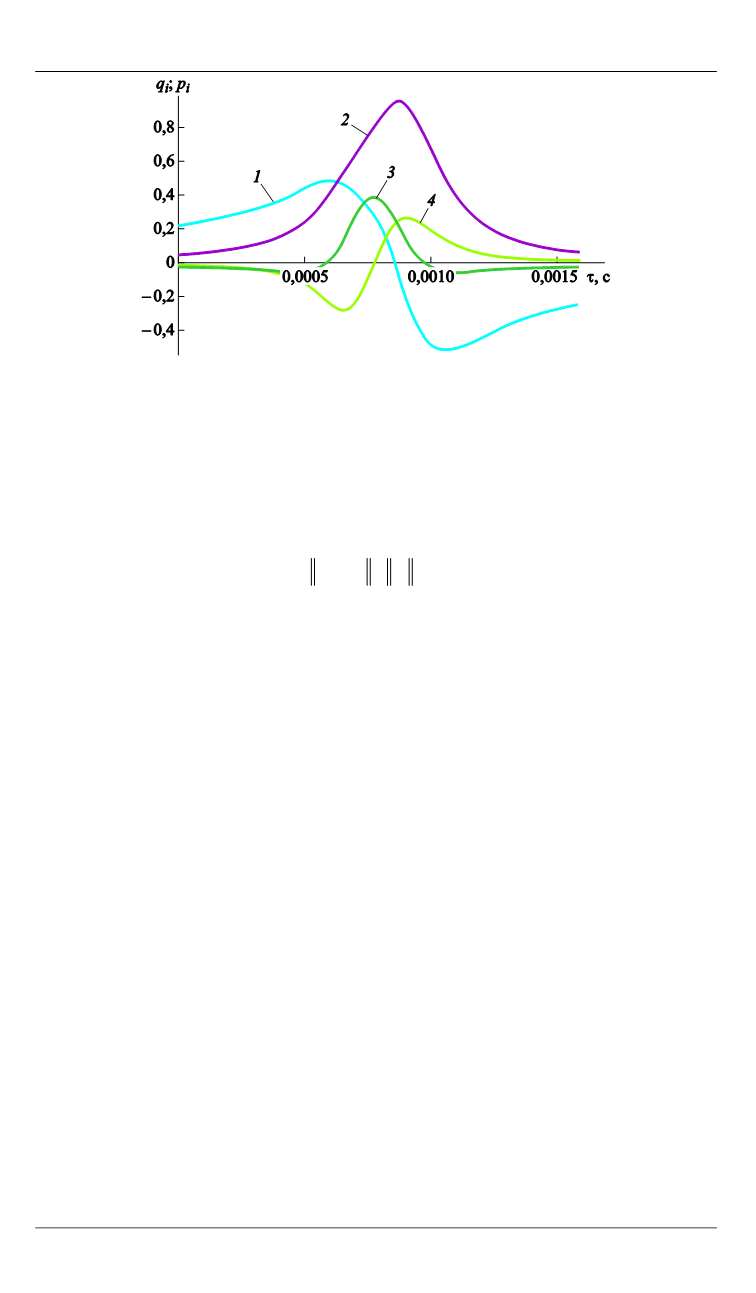
Зависимости
1, 2,
и ,
i
i
i
q p
=
от времени
t
τ = ε
при медлен-
но изменяющейся частоте вынужденных колебаний:
1
—
1
( );
q
τ
2
—
1
( );
p
τ
3
—
2
( );
q
τ
4
—
2
( )
p
τ
Для расчета относительной погрешности параметров, получен-
ных с помощью методик определения параметров, используем ев-
клидову норму вектора:
ˆ /
.
r
= −α α α
При идентификации параметров по методике (18), учитывающей
нелинейность колебаний, получим
(
)
т
1
1
25,168, 1, 995, 1, 283, 1, 488, 0, 004, 0, 011, 9, 989, 12, 004,
30, 006, 0, 006, 0, 01
ˆ
, 2, 990,
3, 0, 002
0, 001,
,
r
=
−
−
−
=
α
а при методике идентификации параметров, не учитывающей нелиней-
ность (коэффициент нелинейности в данном случае отсутствует), —
(
)
т
2
2
25,310, 2, 251, 1, 629, 2, 096, 1, 257, 1, 061, 10, 414, 10,819,
30,111, 0, 287, 0,117, 0, 079 ,
0, 05
,
.
ˆ
1
r
−
=
=
−
α
Проведенные вычислительные эксперименты подтверждают зна-
чительное повышение точности определения параметров при исполь-
зовании предложенной методики идентификации параметров, учиты-
вающей нелинейность.
При проведении идентификации параметров по методу наимень-
ших квадратов (13), обрабатывая сразу весь массив измерений, полу-
чаем
(
)
3
т
3
25,177, 1,998, 1, 277, 1, 491, 0, 017, 0, 021, 9,992, 12, 003,
30, 008, 0, 007, 0, 013, 0, 001 2,
ˆ
,
,
956
0, 002,
r
−
−
=
=
−
α
















