
С.А. Черников, Сюэ Юнцзя
2
Инженерный журнал: наука и инновации
# 10·2017
демпфера рассматривается путем проведения прямых испытаний.
В работе [1] показано определение оптимальных параметров методом
осреднения. В предлагаемой работе эта задача решена методом ми-
нимизации максимального значения амплитудно-частотной характе-
ристики (АЧХ) податливости объекта демпфирования во всем час-
тотном диапазоне [5, 9].
В качестве объекта демпфирования рассмотрим одноосный гиро-
стабилизатор индикаторного типа. Тороидальная полость демпфера
полностью заполнена вязкой несжимаемой жидкостью (рис. 1). Пред-
положим, что ось симметрии полости совпадает с осью стабилизации.
Введем цилиндрическую систему координат с осью
,
z
направленной
по оси симметрии демпфера, и полярными координатами
r
и
в плоскости, перпендикулярной оси
.
z
Поскольку полость, заполнен-
ная жидкостью, имеет форму тора, траекториями движения частиц
жидкости являются концентрические окружности. В этом случае век-
торы абсолютной скорости жидкости
v
удовлетворяют условиям:
,
.
r
z
v v v v
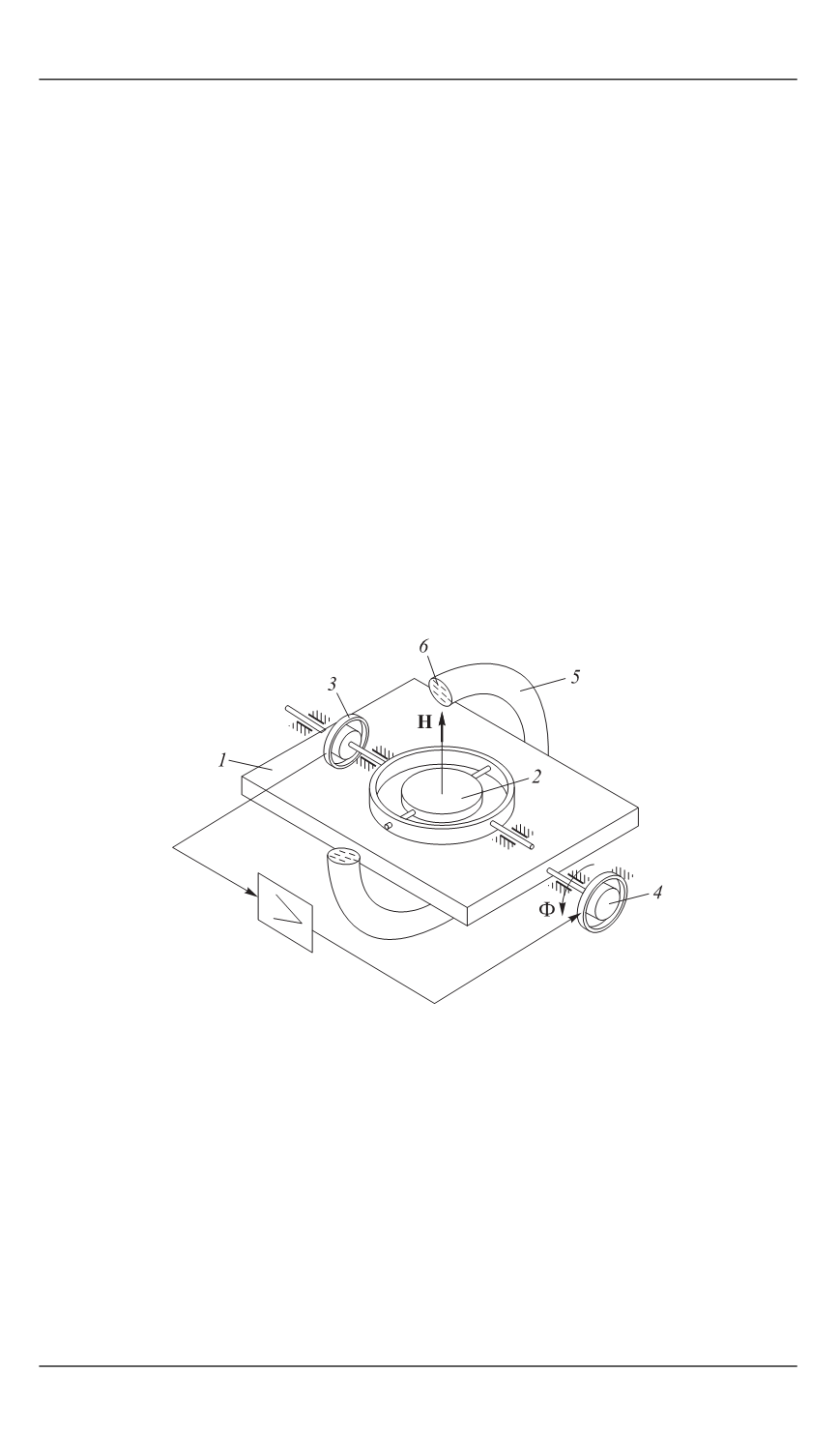
Рис. 1.
Одноосный индикаторный гиростабилизатор
с жидкостным демпфером:
1
— платформа;
2
— гироскоп;
3
— датчик угла;
4
— дат-
чик момента;
5
— жидкостный демпфер;
6
— вязкая жид-
кость;
Н
—
собственный кинетический момент гироскопа
Тогда уравнение движения гиростабилизатора относительно оси
стабилизации можно записать в виде
ж
,
A K M v M
(1)
















