
И.А. Пономарева
4
Инженерный журнал: наука и инновации
# 7·2017
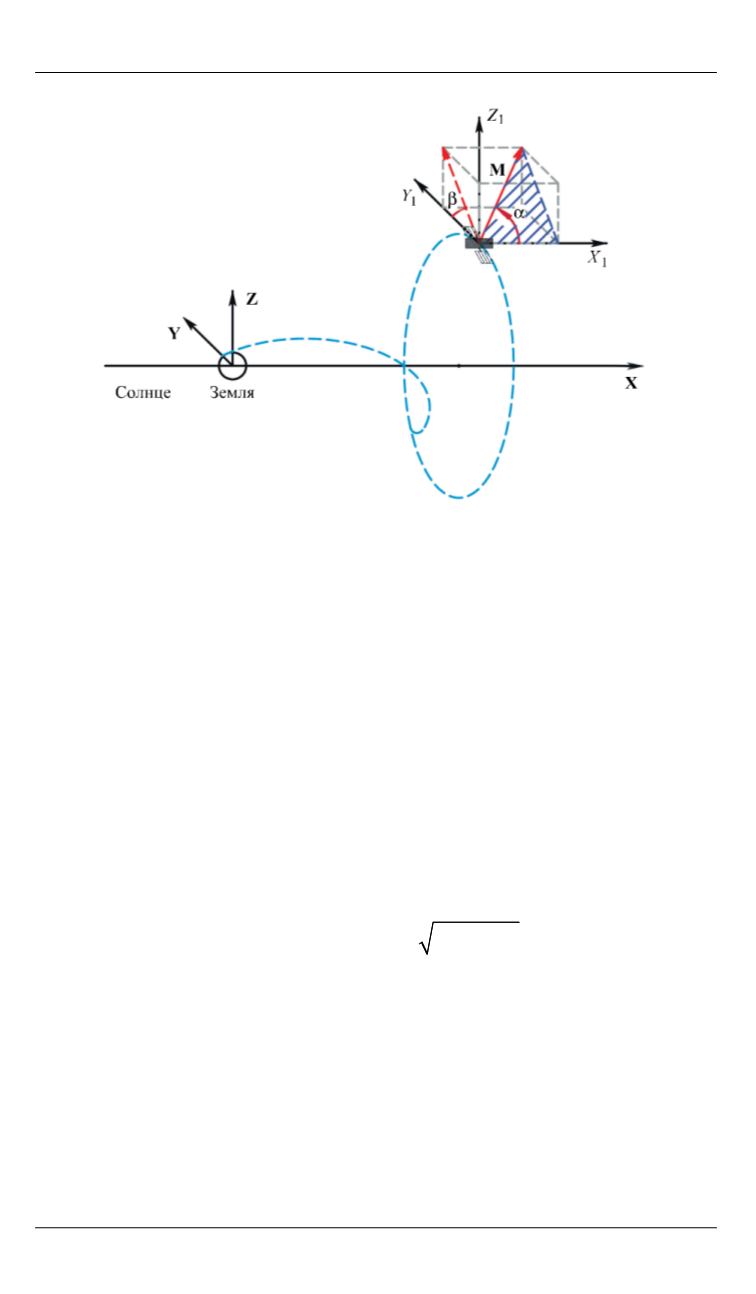
Рис. 2.
Положение углов
и
, определяющих направление реализации
корректирующего импульса во вращающейся системе координат
Таким образом, базовую задачу ставим в формулировке: опреде-
лить параметры маневра
, ,
V
M
в заданный момент времени
м
t
, обеспечивающие максимальное время пребывания КА в заданной
окрестности точки либрации
м
,
max
T t
M
(1)
при наличии ограничений
min
max
,
V V V
min
max
,
0 2 .
Метод расчета параметров маневров на основе квазиньюто-
новского метода оптимизации.
Базовую задачу можно представить
в виде задачи минимизации
м
, ,
,
( )
,
min
V
F
T t
M
M M
(2)
при ограничениях
min
max
,
V V V
min
max
,
0
2 .
Согласно классификации оптимизационных задач — это мини-
мизация с простыми ограничениями. В связи с тем что задача имеет
малую размерность (
n
= 3) и отсутствует возможность аналитическо-
го вычисления производных функции
( ),
F
M
для численного реше-
ния оптимизационной задачи применяем квазиньютоновский метод с
конечно-разностной аппроксимацией производных [5].
Методы ньютоновского типа основаны на учете информации о
кривизне минимизируемой функции, которая содержится в матрице
















