
А.Ю. Бушуев
2
Инженерный журнал: наука и инновации
# 1·2017
При изучении движения панелей рассматривается движение цен-
тра масс каждой панели в глобальной системе координат.
Анализ математической модели.
Анализ динамики процесса
раскрытия, представленной в работе [11], показал, что раскрытие про-
исходит медленно и инерционные силы малы. Следовательно, для мо-
делирования процесса раскрытия можно использовать стационарные
уравнения. Для построенной математической модели в работе [12]
определены оптимальные радиусы роликов, которые обеспечивают за-
данную последовательность фиксации звеньев с учетом дополнитель-
ных углов поворота, вызванных деформациями тросов.
Для создания гибкой системы раскрытия, сохраняющей надежное
раскрытие при различных возмущениях, используются кинематиче-
ские соотношения, представленные в работе [12]. Из анализа кинема-
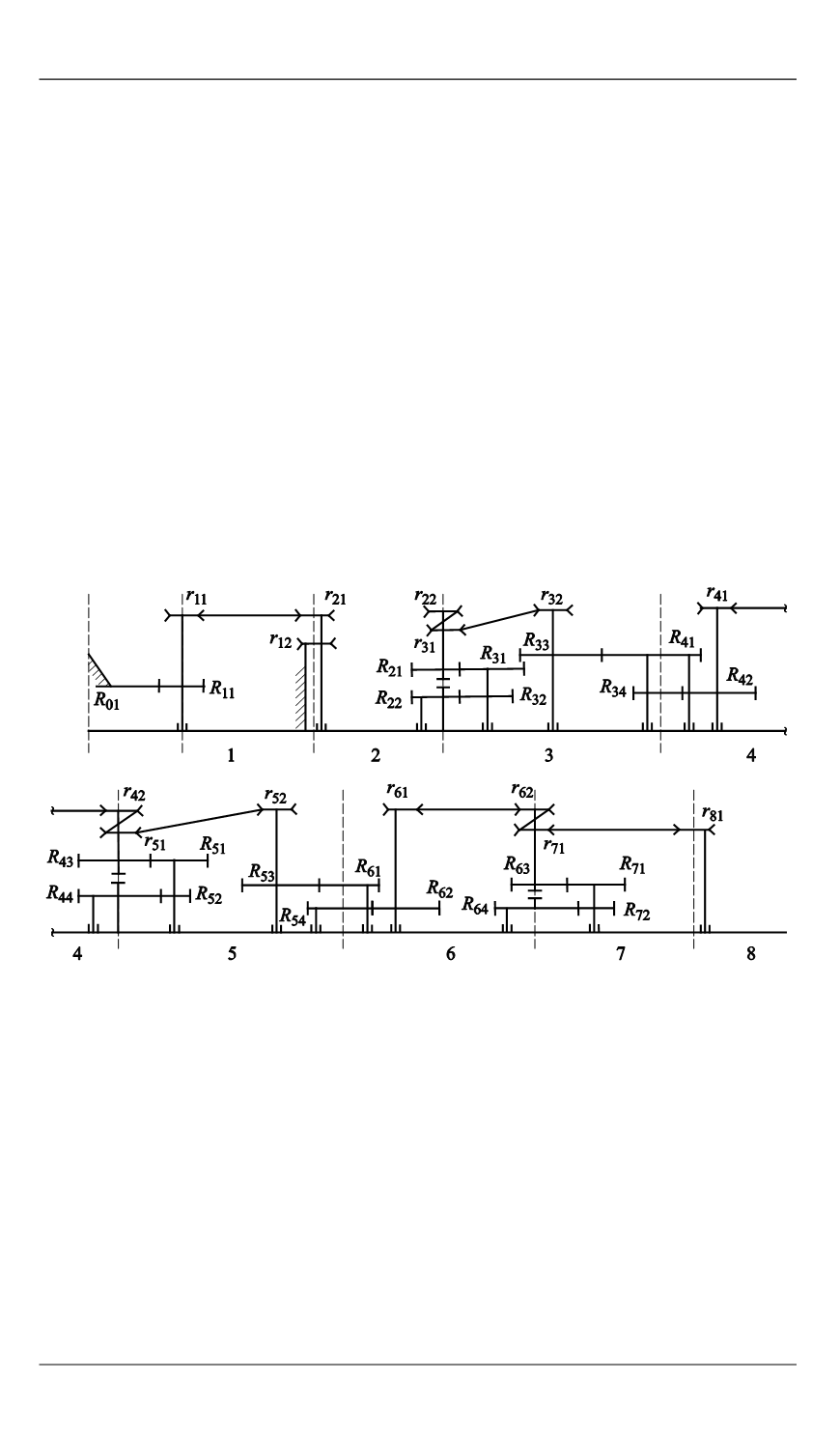
тической схемы системы раскрытия (рисунок) определяются относи-
тельные углы
ij
β
поворота звеньев в зависимости от угла поворота
первого звена.
Кинематическая схема тросовой системы синхронизации:
r
— радиус роликов;
R
— радиус начальной окружности шестерни редуктора
Для расчета передаточных отношений используются основная
теорема зацепления (теорема Виллиса), описанная в работе [14],
и исходные параметры конструкции:
11 21
12 22 31 32 41 42 51 52 61 62
71 81
34 мм;
29 мм;
35, 4 мм;
r r
r r r r r r r r r r
r r
= =
= = = = = = = = = =
= =
2
;
kl
kl
R mz
=
















