
А.Н. Клишин, О.С. Швыркина
6
Инженерный журнал: наука и инновации
# 9·2016
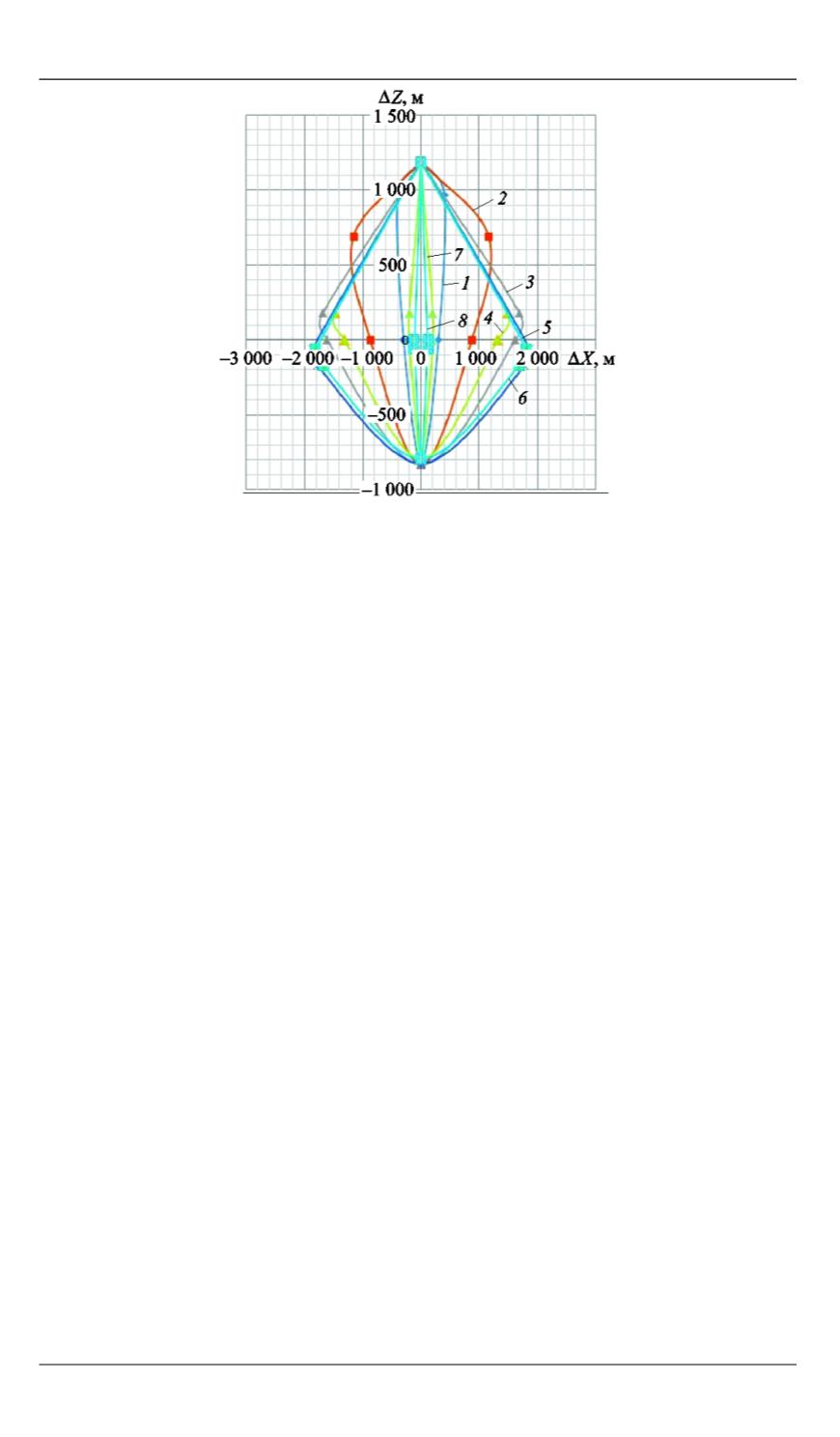
Рис. 3.
Зоны достижения целей при
K
φ
= 10:
1
— 0,5;
2
— 0,6;
3
— 0,7, верхняя граница;
4
— 0,7,
нижняя граница;
5
— 0,8, верхняя граница;
6
— 0,8,
нижняя граница;
7
— 0,7, верхняя граница;
8
— 0,8,
верхняя граница
Аналогично построены зоны достижения целей при постоянном
значении
K
χ
и переменных значениях
K
φ
.
Полученные результаты
приведены на рис. 4.
Увеличение коэффициента
K
φ
приводит к увеличению диапазона
поражения цели по оси Δ
XO
, также происходит смещение центра до-
стижения по оси Δ
XO
к б
î
льшим значениям и увеличению диапазона
по оси Δ
Z
. Помимо этого площадь зоны достижения увеличивается.
В результате можно сделать вывод, что от значений коэффициен-
тов
K
φ
и
K
χ
зависят форма и размер зоны достижения цели, и невоз-
можно подобрать определенные постоянные коэффициенты, при ко-
торых будет поражена вся номинальная область. Поэтому необходи-
мо найти такие функции
K
φ
=
f
φ
(Δ
X
, Δ
Z
) и
K
χ
=
f
χ
(Δ
X
, Δ
Z
), при
которых возможно получить максимальную зону достижения цели.
Рассмотрим сечение зоны достижения цели вдоль оси ΔZO относи-
тельно постоянного значения Δ
X
. Результаты представлены на рис. 5.
Промах по сечению Δ
Z
в зависимости от коэффициента
K
φ
при
постоянном значении
K
χ
изменяется по одному закону. Наблюдается
точка наименьшего промаха, после которого промах начинает сильно
возрастать, и чем больше коэффициент
K
φ
, тем выше скорость воз-
растания. Поскольку допустимый промах, при котором принимали,
что цель достигнута, равен 30 м, число точек достижения оказывает-
ся больше при меньших значениях коэффициента.
















