
А.Н. Клишин, О.С. Швыркина
4
Инженерный журнал: наука и инновации
# 9·2016
Рассчитывали углы тангажа, крена и рыскания соответственно:
sin
cos ;
ϑ = ω γ + ω γ
y
z
sec ( cos
sin );
ψ = ϑ ω γ −ω γ
y
z
tg ( cos
sin ),
γ = t − ϑ t γ −t γ
x
y
z
где
,
,
ω ω ω
x
y
z
— угловые скорости вращения.
На основе приведенной модели в программной среде С++
разработан вычислительный комплекс. В качестве метода
интегрирования выбран метод Рунге — Кутты четвертого порядка. В
качестве опорной траектории принимали движение ракеты без
наведения на конечном участке движения.
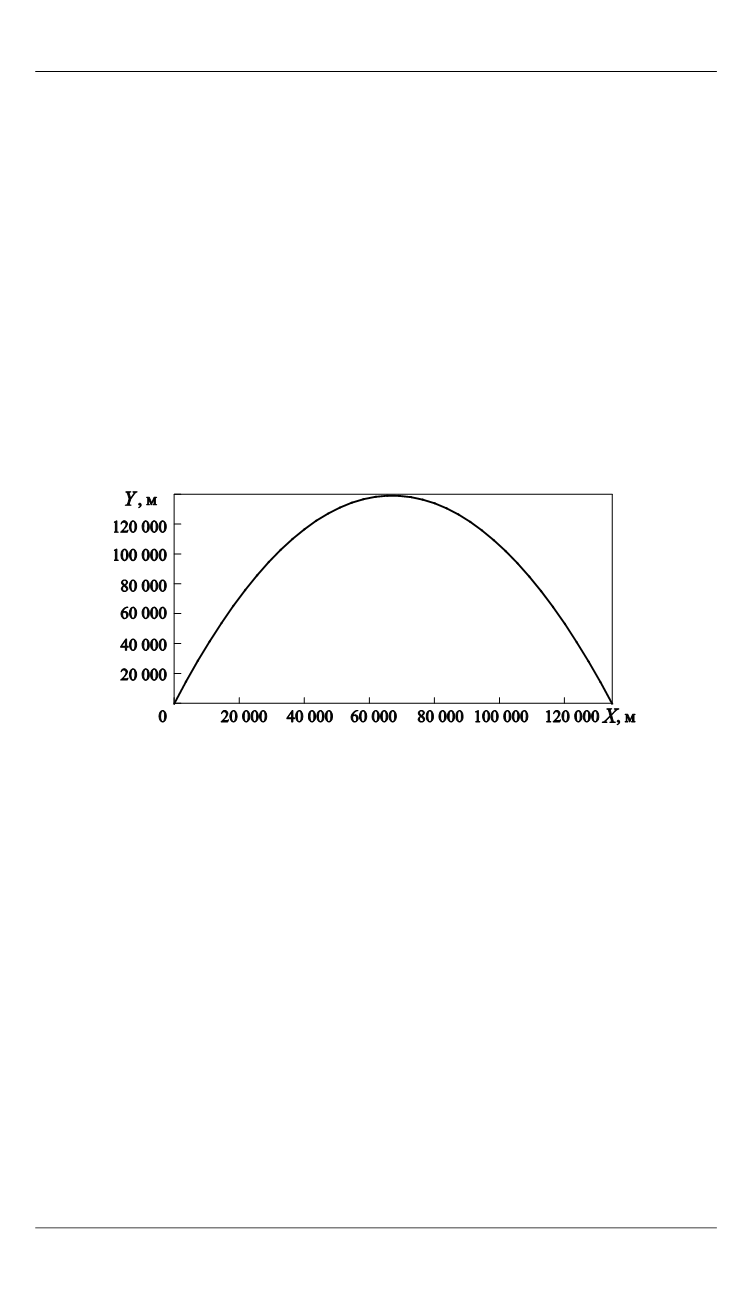
На основании результатов расчетов построена траектория
движения ЛА (рис. 1).
Рис. 1.
Траектория движения ЛА
Максимальная высота полета ЛА 130 км, дальность полета 134 км.
До момента времени
t
= 32 с, соответствующего высоте полета
h
= 20 км, работает двигатель и идет управление газодинамическими
рулями на программный угол тангажа. В момент времени
t
= 54 с
высота полета составляет 50 км. Влияние атмосферы становится не-
существенным, и ОУ влетает опять в зону действия атмосферы в мо-
мент времени
t
= 304 с.
В рамках поставленной задачи будем рассматривать движение на
конечном участке траектории, когда начинается этап самонаведения.
Наведение начинается с высоты 10 км, в данный момент значение
угла атаки стремится к нулю (~5°).
Рассмотрим наведение. Примем за область достижения цели со-
вокупность точек, которые ОУ может поразить. В зависимости от ме-
тода наведения, а также принятых коэффициентов наведения зона
достижения цели будет изменяться. На элемент управления ЛА
накладываются ограничения по предельному отклонению рулей, что
















