
Алгоритм выбора коэффициентов пропорционального метода наведения…
Инженерный журнал: наука и инновации
# 9·2016 9
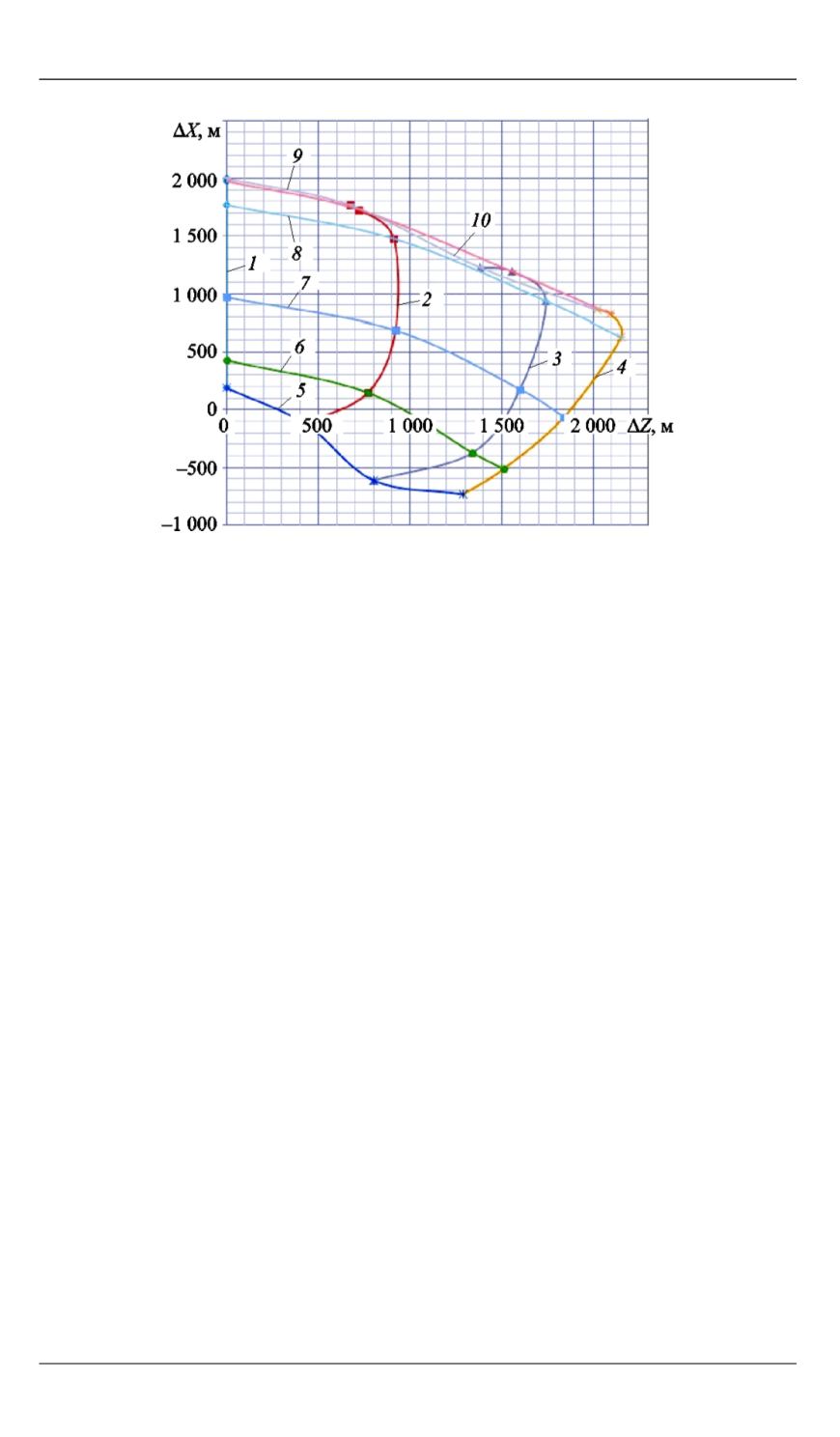
Рис. 6.
Опорные точки построения плоскостей:
1
–
4
—
K
χ
равно 0,5, 0,6 0,7 и 0,8 соответственно;
5
–
10
—
K
φ
равно 5, 7, 10, 15, 20 и 30 соответственно
Видно, что коэффициенты
K
φ
и
K
χ
зависят как от ∆
X
, так и от ∆
Z
.
При этом при постоянном значении одного коэффициента второй
описывает схожие линии.
Принимая данные точки за опорные, строим графики функций
f
φ
(Δ
X
, Δ
Z
) и
f
χ
(Δ
X
, Δ
Z
). Примеры изображения полученных плоско-
стей функций представлены на рис. 7.
Затем, вычисляя через полученные функции коэффициенты наве-
дения, строим зоны достижения цели и добиваемся максимального
покрытия. Изменяя плоскости, описывающие данные функции, и при
тех же опорных точках, изменяем и зоны достижения цели.
Увеличивая число рассматриваемых точек, увеличиваем частоту
«сетки» известных величин, а значит, тем самым увеличиваем точ-
ность уравнения, описывающего плоскость.
Этапы полученного алгоритма.
1.
Для заданных коэффициентов наведения определяется положе-
ние цели, при котором промах будет наименьшим, и выбираются
наиболее отдаленные координаты цели.
2.
Из полученных точек расположения цели формируется плос-
кость, описывающая зависимость коэффициентов наведения от удале-
ния цели от точки прицеливания. На ее основании выбираются опорные
точки и получаются эмпирические зависимости коэффициентов про-
порционального метода наведения от удаления цели от прицельной
точки.
















