
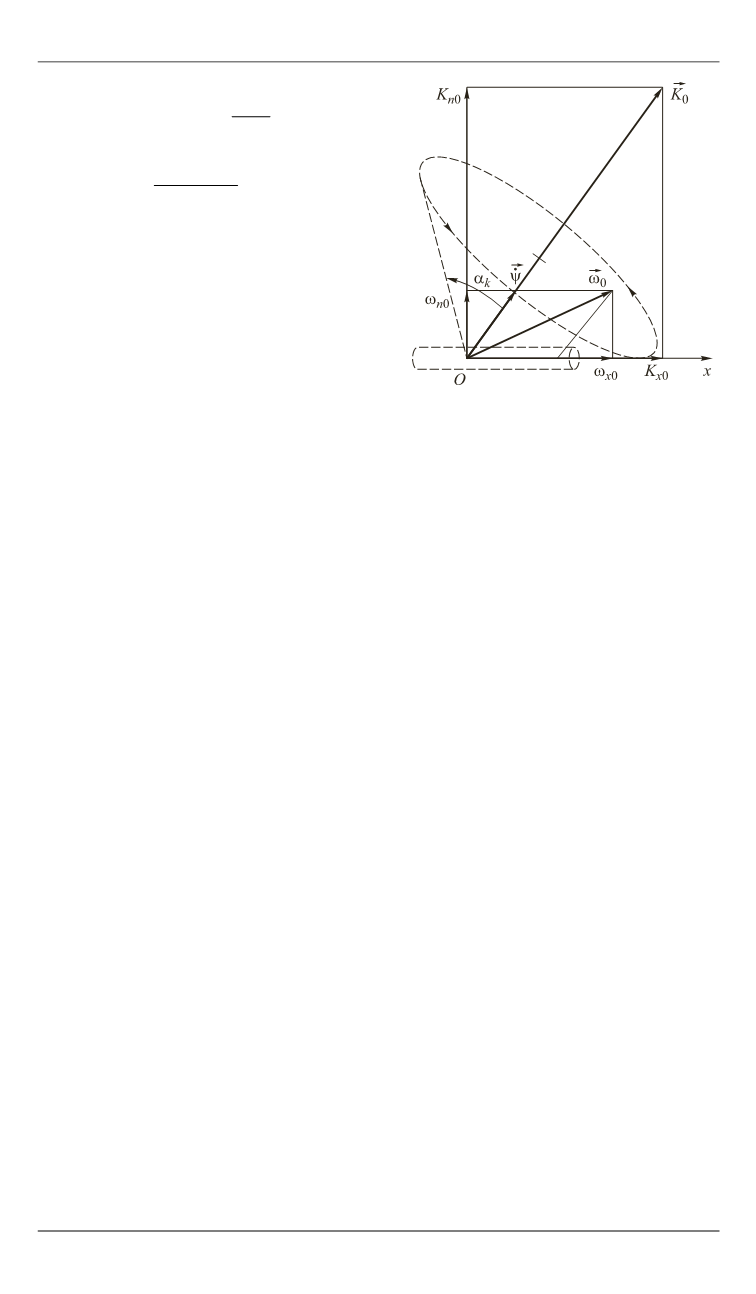
Оценка точности алгоритма видеонавигации
Инженерный журнал: наука и инновации
# 7
2016
3
0
0
0
arcsin
;
,
.
cos
n
k
x x
n
k
K
K
I
t
I
(1)
Здесь
0
n
— поперечная угловая
скорость,
град/с
;
0
,
x
0
,
y
0
z
—
проекции угловой скорости,
град/с;
0
n
K
и
0
x
K
— поперечная и про-
дольная проекции вектора кинети-
ческого момента орбитальной сту-
пени,
2 1
кг м c ;
0
K
— вектор
кинети-ческого момента орбиталь-
ной ступени,
2 1
кг м c ;
n
I
и
x
I
— поперечный и продольный мо-
менты инерции орбитальной ступени,
2
кг м ;
k
— угол полурас-
крытия конуса прецессии,
град ;
— угловая скорость прецессии,
град/с;
— угол прецессии,
град ;
t
— время, с.
При этом наноспутник отдаляется от орбитальной ступени. Зави-
симость координат его центра масс от времени можно найти по фор-
мулам
2
2
2 0;
2 3
0;
0,
x y
y x
y
z
z
(2)
где
,
x
,
y
z
— ускорения наноспутника,
2
м/с ;
,
x
y
— скорости
наноспутника, м/с;
,
y
z
— координаты наноспутника, м;
— орби-
тальная угловая скорость,
град/с.
Угловая скорость в данной задаче может быть найдена по после-
довательности нескольких кадров.
Начальными условиями для моделирования являются:
1)
высота полета
= 380км,
H
орбита — круговая;
2)
моменты инерции орбитальной ступени
2
=14 406 кг м ,
n
I
2
= 2 548 кг м ;
x
I
3)
моменты инерции наноспутника
2
= 0,0146 кг м ;
n
I
=
x
I
2
= 0,00405 кг м ;
4)
составляющие вектора угловой скорости орбитальной ступени
при моделировании
0
0
0
= –2,5 град/с,
= 1 град/с,
= 1 град/с.
x
y
z
Рис. 2.
Регулярная прецессия
орбитальной ступени
















