
Е.А. Сухов, Б.С. Бардин
6
Инженерный журнал: наука и инновации
# 5·2016
опорные решения системы (1) в окрестности гиперболоидальной пре-
цессии (2) в виде сходящихся рядов по малому параметру. В общем
случае существуют два семейства периодических решений данного ти-
па с периодами, близкими к
1
1
2
T
π=
ω
и
2
2
2
T
π=
ω
, где
1
ω
и
2
ω
— частоты
малых линейных колебаний (
1
2
ω > ω
). В предлагаемой работе в каче-
стве опорных выбираются так называемые короткопериодические ре-
шения с периодами, близкими к
1
T
, существование которых всегда га-
рантируется теоремой Ляпунова о голоморфном интеграле [7].
В качестве малого параметра выбрано отклонение полной меха-
нической энергии
h
∆
от ее значения на гиперболоидальной прецес-
сии. На втором этапе опорные решения были численно продолжены
по параметрам с помощью приведенного алгоритма. В окрестности
опорного ляпуновского решения при значениях константы энергии
8
4
1 10
1 10
h
−
−
⋅
≤ ≤ ⋅
приращения параметров выбирали исходя из соот-
ношения
i
h
π ≈
. При
4
1 10
h
−
> ⋅
выбор приращений проводили в со-
ответствии с формулами (6). Погрешность (3) получаемых решений
не превышала
5
1 1 .0
−
ε = ⋅
Для спутников с геометрией масс пластинки
(
2,
0,3)
α = β =
и
близкой к стержню
(
0,1,
0, 3)
α = β =
в аналитическом виде найдены
ляпуновские опорные решения и численно построены однопарамет-
рические семейства периодических решений. В качестве параметра
использовали константу энергии
h
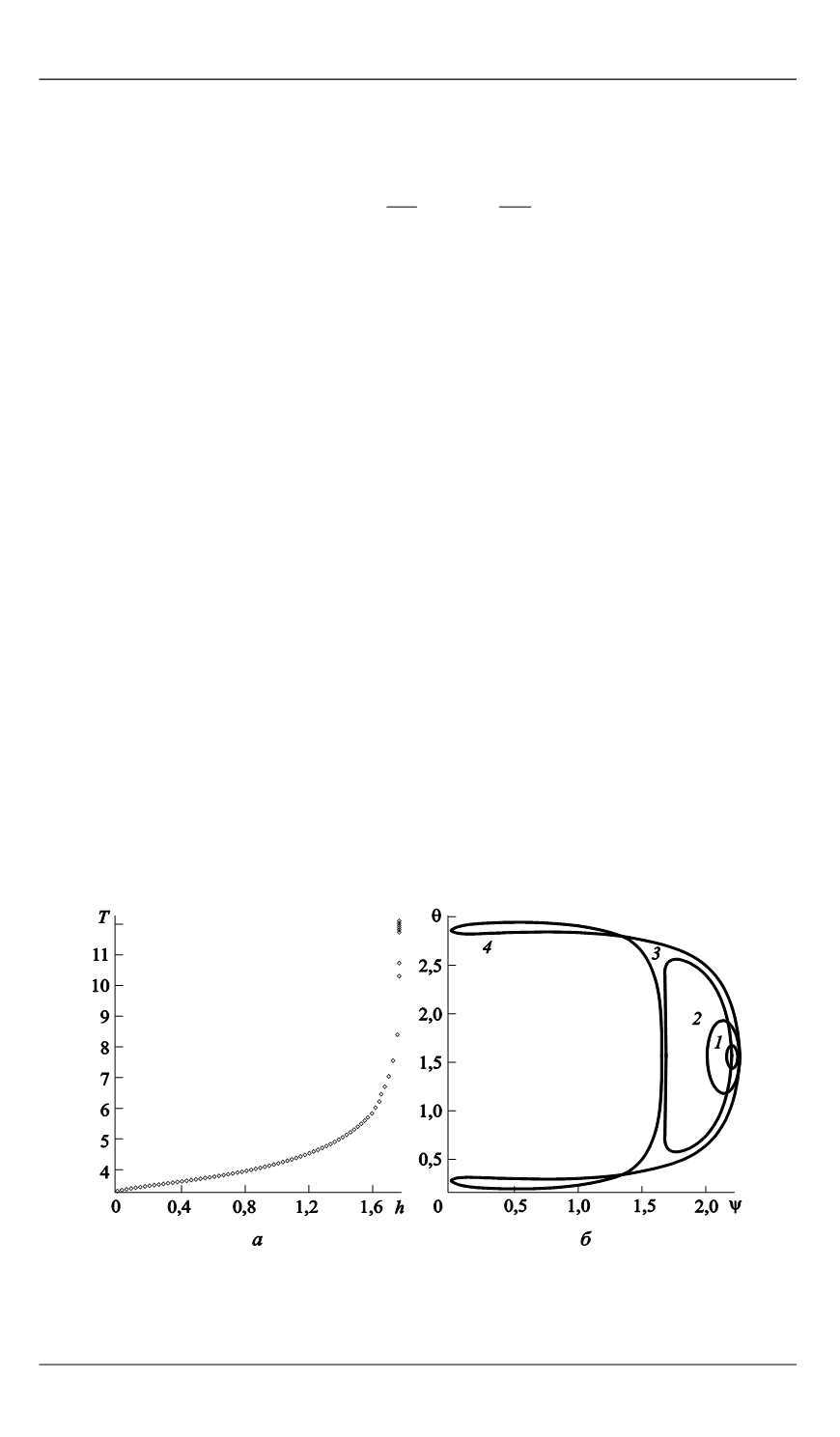
. На рис. 2 и 3 для принадлежащих
полученным семействам решений приведены зависимости периода от
константы энергии и характерные формы траекторий в проекции на
плоскость
ψ − θ
.
Рис. 2.
Зависимость периода
T
от константы энергии
h
(
а
) и характерные формы
траекторий в проекции на плоскость ψ – θ (
б
) для спутника-пластинки:
1
—
h
= 0,02568207654,
Т
= 3,402713243;
2
— 0,2256820665, 3,537270619;
3
— 1,22568204,
4,69963124;
4
— 1,770678236, 12,1523945


















