
Численно-аналитическое построение семейства периодических движений…
Инженерный журнал: наука и инновации
# 5·2016 5
Исходя из разложения (4) и учитывая порядок
ε
, погрешности
0
z
∆
предыдущего шага, значения приращений можно подобрать так,
что будут выполнены следующие оценки:
~ ;
~ .
∆ ∆ ε ∆ ∆ ε
i
h
p i
z h
z p
(5)
В программной реализации условие
const
π =
обеспечивается за
счет объединения последовательных шагов в группы конечной длины, в
пределах которых не применяется корректор, а приращения параметров
остаются постоянными. В этой задаче длина группы составляет 4 шага.
После выполнения последнего шага группы делается проверка на
соответствие критерию точности
( , ) .
z h p
∆ < ε
Если данный критерий
выполняется, то, учитывая оценки (5), вычисляют новые значения
приращений по формулам
;
,
i
i
h
p
h
p
z
z
ε
ε
∆ = ∆ =
∆
∆
(6)
а затем осуществляют этап корректора, на котором уточняется
решение, полученное на последнем шаге. Если же критерий не
выполняется, то приращение варьируемого параметра делится
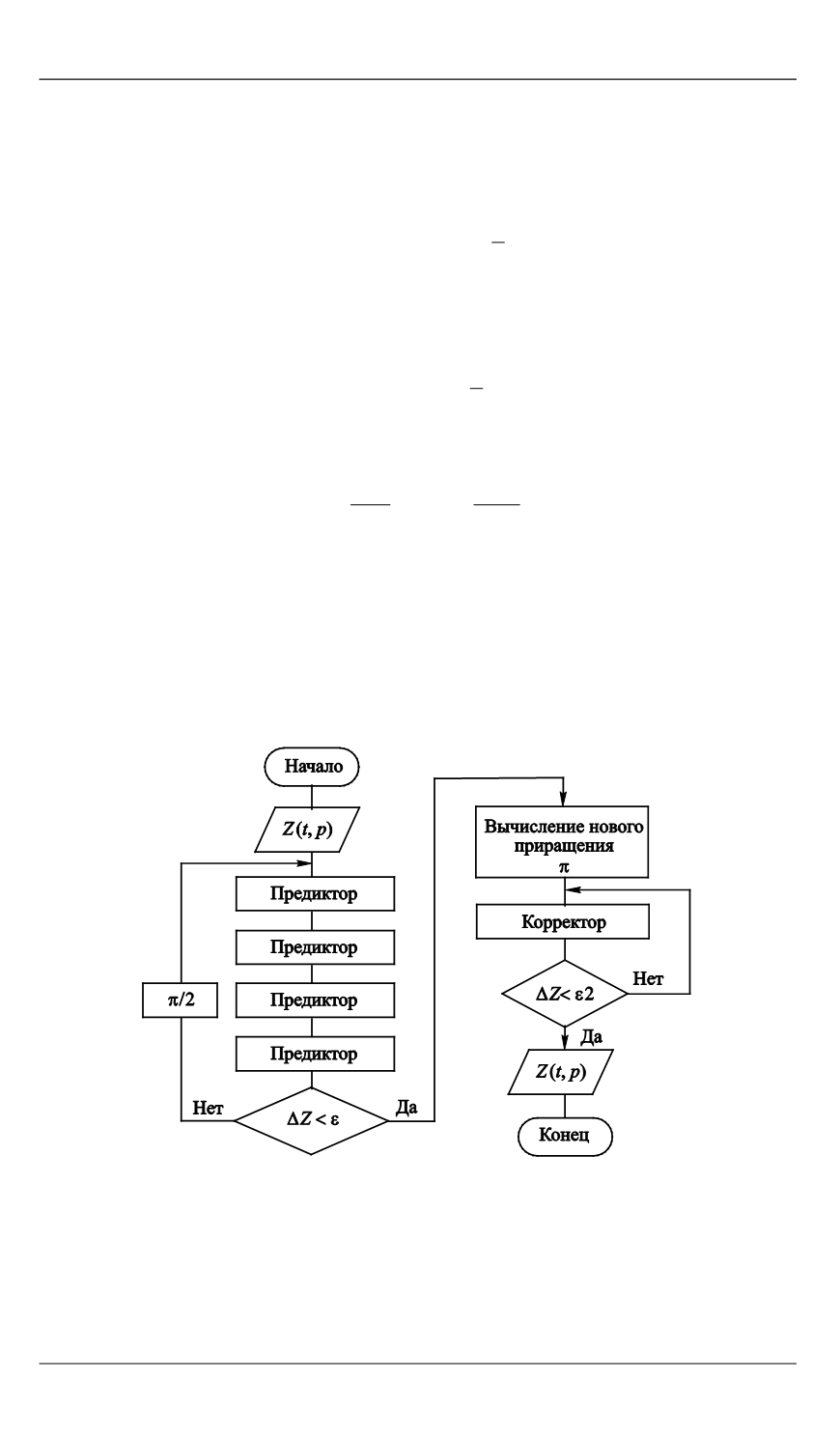
пополам и выполнение последней группы шагов повторяются. Блок-
схема программной реализации описанной части алгоритма
представлена на рис. 1.
Рис. 1.
Блок-схема алгоритма вычисления нового периодического решения:
ε2 — задаваемая величина, определяющая точность работы корректора
Численно-аналитическое построение семейств периодических
движений симметричного спутника в случае его гиперболоидаль-
ной прецессии.
Построение семейств периодических решений прово-
дили в два этапа. На первом этапе по методу Ляпунова были найдены


















