Методика выявления и оценки сближений космического аппарата с объектами космического мусора

5 / 16

Методика выявления и оценки сближений космического аппарата…
Инженерный журнал: наука и инновации # 4·2016 5
Найдем области, для которых выполняется условие ∆z <∆ (рис. 1).
Используя формулы сферической геометрии, вычислим угол γ между
плоскостями орбит КА и КО:
КO КA КO КA cos cos cos sin sin cos , i i i i γ = − + AΩ
где КO , i КA i — наклонение орбиты КО и КА соответственно; ΔΩ =
= ΩКА — Ω КО (Ω — долгота восходящего узла).
Затем определим аргументы широты встречи (UвстКО, UвстКА) до
линии пересечения плоскостей орбит для КА и КО соответственно:
КA КO
встКO
КO
cos cos cos γ
cos ;
sin sin γ
i i
U
i
+
=
КO КA
встКA
КA
cos cos cos γ
cos .
sin sin γ
i i
U
i
+
=
Далее рассмотрим сферический треугольник (см. рис. 1), образо-
ванный пересечением траекторий сближающихся объектов и сторо-
ной α, которая вычисляется по формуле
*
КА tg / ,r α = ∆
где *
КА r — длина радиуса-вектора КА на линии пересечения плоско-
стей.
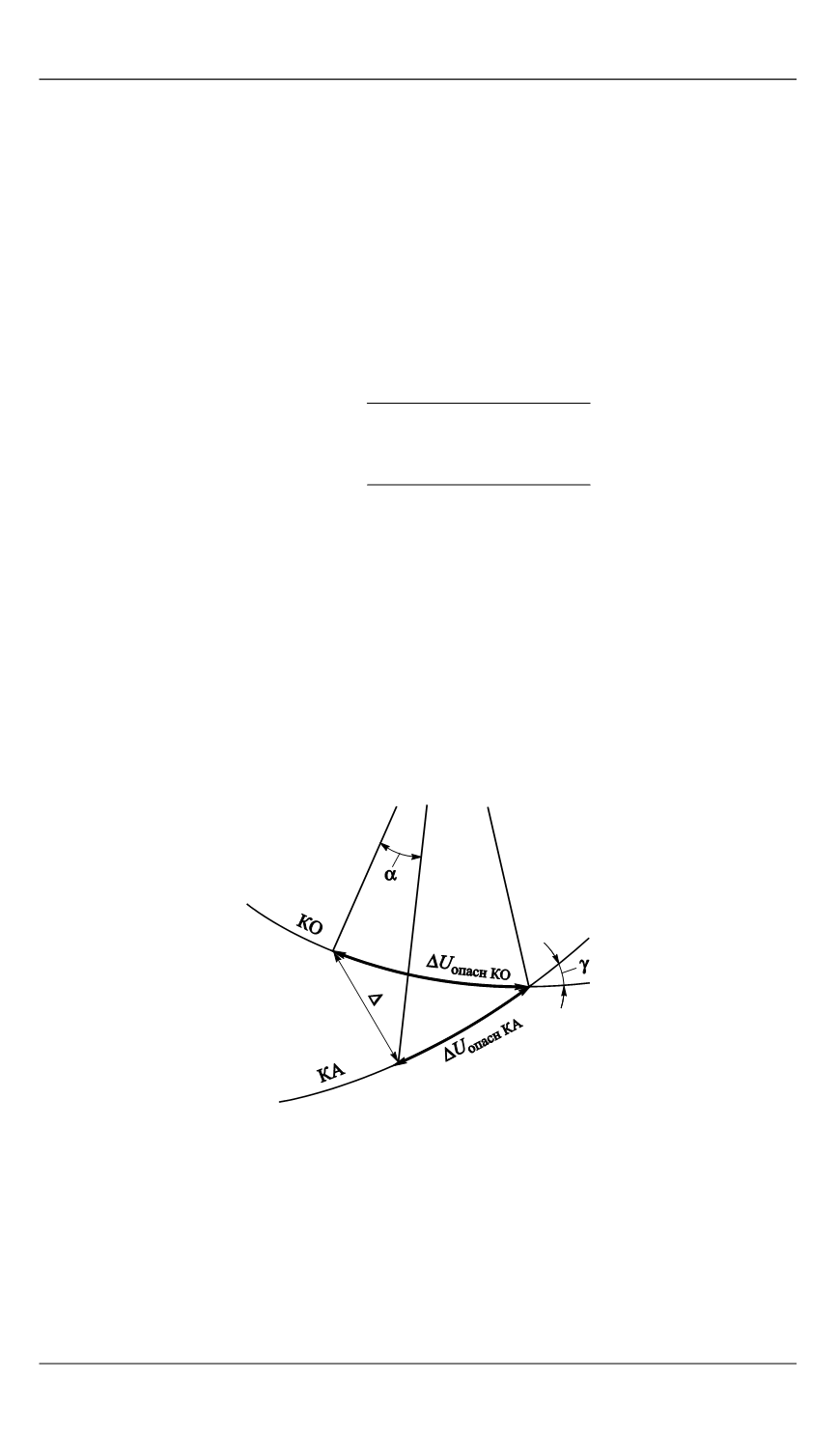
Рис. 1. Область пересечения орбит КА и КО
Угол между стороной α и траекторией КА — прямой. Область
возможных сближений для КА может быть охарактеризована следу-
ющим выражением:
{ } [ ]
риск2 встКА опаснКА встКА опаснКА, U U U U U = − ∆ + ∆ ,