
А.А. Баранов, М.О. Каратунов
8
Инженерный журнал: наука и инновации
# 4·2016
достаточно велико, это приводит к смещению точки сближения. Дан-
ный эффект усиливается с ростом эксцентриситета рассматриваемых
орбит и уменьшением угла между плоскостями.
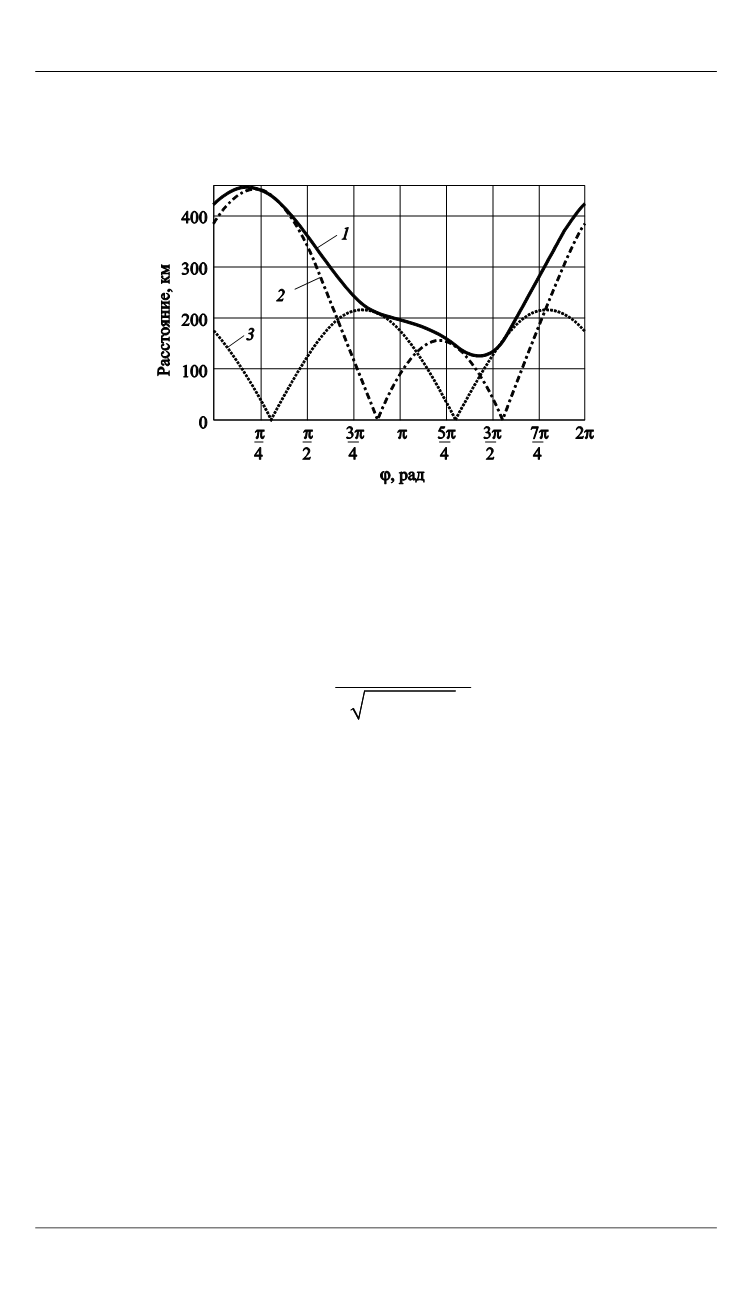
Рис. 2.
Зависимости абсолютного расстояния между ор-
битами (
1
), расстояний в радиальном (
2
) и боковом (
3
)
направлениях от угловой координаты
Найдем точку минимального расстояния между орбитами, для
этого исследуем функцию Δ
D
(φ) на экстремумы:
φ
φ
φ
2
2
;
r r z z
D
r
z
∆ ∆ + ∆ ∆ ′
′
∆ =′
∆ + ∆
0
0
0
cos φ (
2 ) sin φ;
r
t
r
V
r
V
ϕ
∆ = ∆
( ∆ ( ∆
′
0
0
cos φ sin φ.
z
z
V
z
ϕ
∆ = ∆
− ∆
′
После некоторых алгебраических преобразований получим необ-
ходимое условие экстремума в следующем виде:
2
2
1
1
2
3
4
cos φ sin φ sin φ cos φ sin φcos φ 0
K
K
K
K
K
−
+
+
+
=
, (4)
где
1
0 0
0 0
0 0
2
r
t
r
z
K r V V V z V
= −∆ ∆ − ∆ ∆ + ∆ ∆
;
(
)
2
2
2
0
0 0
0
2
3
2 ;
t
t
K r
r V V
= ∆ + ∆ ∆ + ∆
(
)
3
0 0
0 0
2
;
r
t
r
K r V V V
= ∆ ∆ + ∆ ∆
(
)
2
2
2
2
4
0
0
0
0
0
2
.
r
t
z
K V r
V V z
= ∆ − ∆ + ∆ + ∆ − ∆
Решив уравнение (4), получим возможные положения
*
i
ϕ
экстре-
мумов, из которых путем непосредственного сравнения значений
функций
*
( )
i
D
∆ ϕ
определяется положение абсолютного минимума
















