Математическая модель информационно-статистического синтеза беспилотных летательных аппаратов по экспериментальным данным

7 / 12

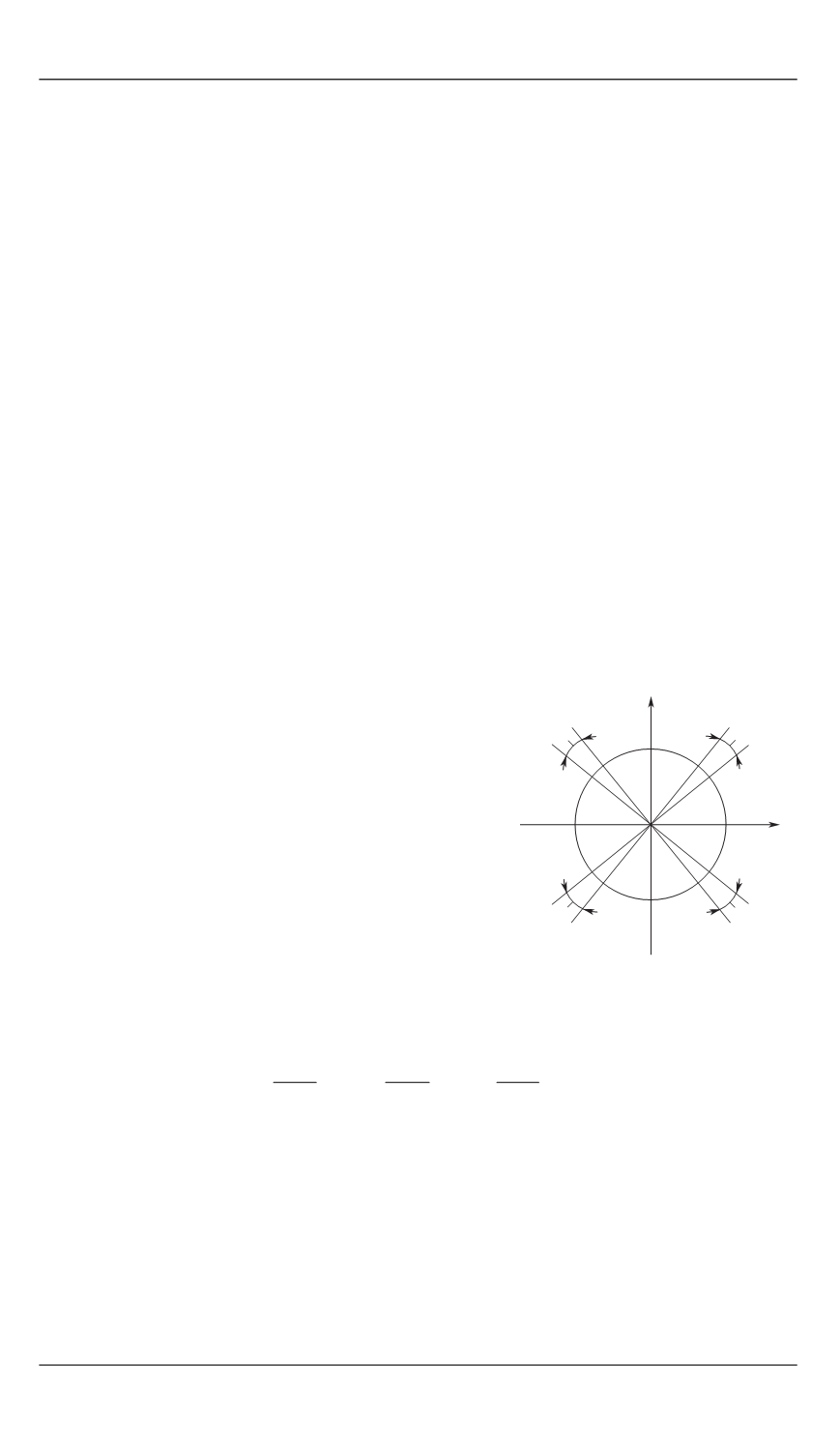
Математическая модель информационно-статистического синтеза…
Инженерный журнал: наука и инновации # 22016 7
формировать не только по статистическим, но и по основным физи-
ческим критериям, таким как промах, угол подлета к цели, скорость
подлета и т. д. [5].
Корректировка аэродинамической модели по результатам
аэродинамических продувок. Представим векторный критерий
оценки качества БЛА следующим образом [6]:
 2 2 2
1 2 3 ( / 2) ( ) ( ) ( ) ...
cx cy cz J B B B                

2 2
4 ( ) ( ) ,
my mz B B        (12)
где  — промах;  — угол тангажа; i  — весовые коэффициенты,
сумма которых равна 1, i = 1…7.
Предполагается, что задача решается в условиях действия следу-
ющих неконтролируемых факторов:
ω1 = Хц — координата положения цели по оси Х;
ω2 = Yц — координата положения цели по оси Ү;
ω3 = Vц — скорость цели.
Данные аэродинамических продувок имеют следующий состав:
V — скорость БЛА по оси X;
nx — перегрузка по оси X;
ny — перегрузка по оси Y;
nz — перегрузка по оси Z;
δ1, δ2, δ 3, δ 4 — углы отклонения ру-
лей (см. рисунок);
α — угол атаки;
β — угол скольжения;
M – число Маха.
Аэродинамические коэффициенты
БЛА рассчитываются по следующим
зависимостям [7, 8]:
; ; . y x z
x y z
m m m
n G n G n G
с с с
s q s q s q
   (13)
Здесь nx, ny, n z — продольные перегрузки по осям x , y, z соответ-
ственно; / ; / ; / ;
x y z n X G n Y G n Z G   q — скоростной напор,
2 /2.  q V
Для расчета коэффициентов аэродинамических моментов исполь-
зуют уравнения Эйлера:
Углы отклонения рулей БЛА
δ1
δ2
δ4
δ3
Y
Z