Оптимальное проектирование балки с ограничениями на частоту собственных колебаний

4 / 9

А.А. Гурченков, И.М. Герман, А.М. Романенков
4
   
2
1
1
( ) min;
0,
N
i i
i
N
k
i i i
i
x a
x h A



  


  




(11)
где   2
1 ( ) 1 , 1, , .
2
k i i
i i
V V
A h x i N      
   
 
 
Для решения задачи на условный экстремум воспользуемся ме-
тодом множителей Лагранжа [14–17], который дает следующее пра-
вило построения функции ( ): h x
1 ( 1) ( )
2
1
.
N
j
j k k
i i i N
j
j
x A
h h x A
A
 


    

На формуле (12) основано программное решение поиска опти-
мальной толщины балки. Отметим, что система дифференциальных
уравнений (2)–(2') решена методом матричной прогонки.
Результаты. В следующих примерах приведена форма прогиба
балки, зависящая от различных способов закрепления концов балки.
Данные результаты получены с использованием программы, разрабо-
танной на языке C# 5.0 .net framework 4.5.
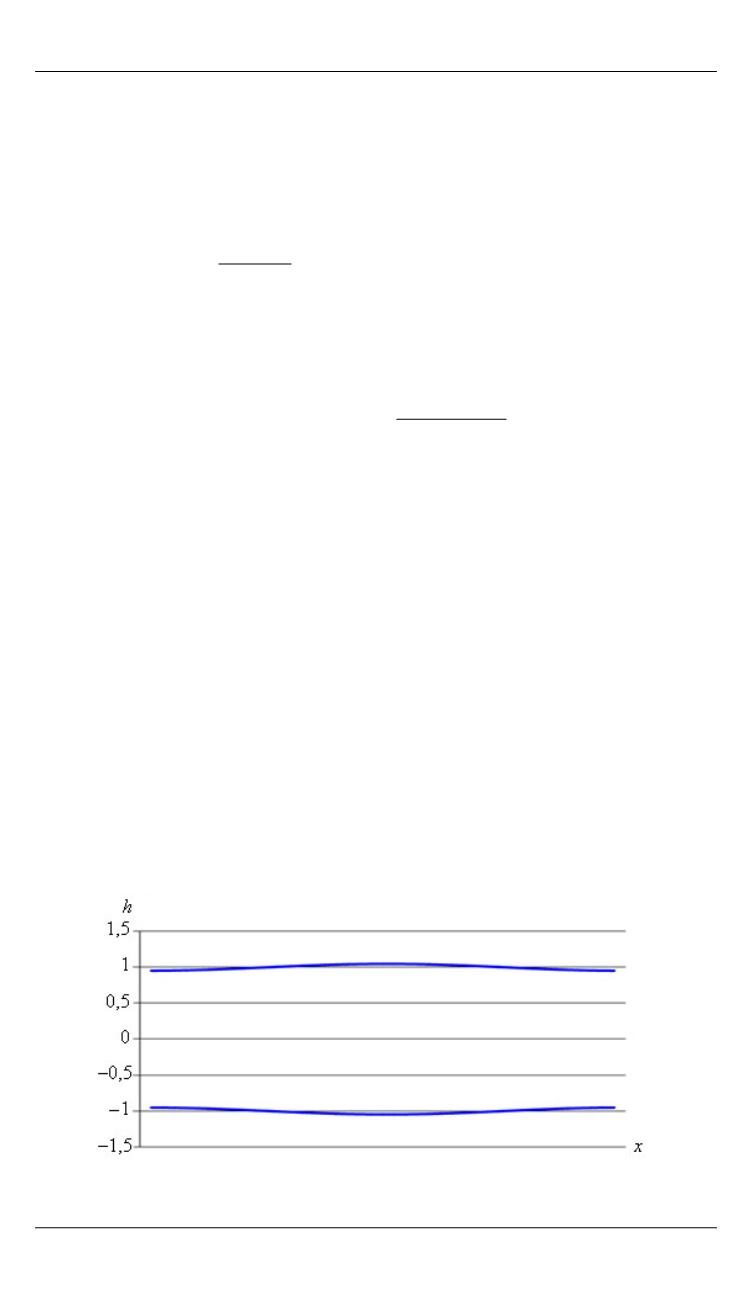
Пример 1. Балка свободно оперта на обоих концах (рис. 1). По
горизонтали на рис. 1 отложена координата x от 0 до 1. С помощью
программы определена толщина балки, а именно функция, значение
которой строго положительно. Кривая, находящаяся в отрицательной
части графика, получена простым отражением верхней кривой. Зна-
чение веса балки, а именно, значение функционала J[h(x)] равно
0,89J0, где J0 — вес балки, рассчитанный без применения метода оп-
тимизации.
Рис. 1