
А.А. Грешилов
16
наилучшей с точки зрения суммы квадратов невязок является комби-
нация 2. Этой комбинации соответствуют три вида деления:
235
U
th
,
рассчитанный относительный вклад которого 35,99 (деление тепло-
выми нейтронами);
235
U
f
, рассчитанный относительный вклад кото-
рого 42,97, и
235
14
U , рассчитанный относительный вклад которого
110,27. Аналогично для остальных методов решения.
В графе «Сумма квадратов невязок» приведены значения суммы
квадратов невязок системы уравнений (15), рассчитанных для ука-
занных в таблице комбинаций видов деления и оценок их вкладов в
суммарную активность изотопов криптона и ксенона.
В графе «Время работы алгоритма, мин» указано в минутах вре-
мя получения оценки вкладов соответствующим методом.
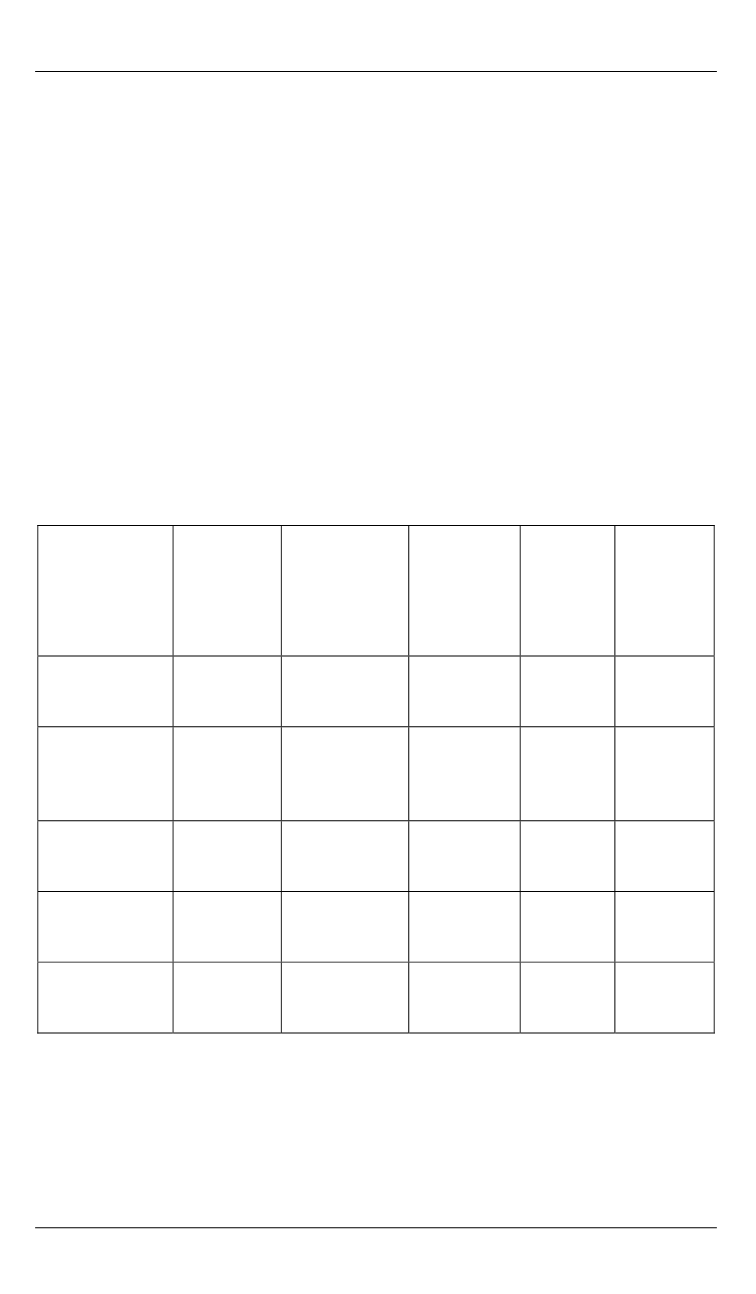
Результаты решения задачи идентификации разными методами (источни-
ком радиоактивности являются
235
U
f
и
235
14
U
, точное решение 100 и 100)
Метод
решения
Номер
комбина-
ции видов
деления
Порядок
числа обу-
словленно-
сти
матрицы
системы
Оценка
решения
Сумма
квадра-
тов
невязок
Время
работы
алгорит-
ма, мин
Регуляриза-
ция
Тихонова
2
6
10
35,99;
42,97;
110,27
751,39
1,46
Квадратич-
ное про-
граммиро-
вание
9
14
10
84,94;
108,18;
0; 0; 10,99
74,97
9,28
Нелинейное
программи-
рование
9
14
10
43,53;
120,76;
0; 0; 0
5096,43
11,95
Архимедова
модель
9
14
10
84,94;
108,18;
0; 0; 10,98
74,97
13,40
Модель с
приоритета-
ми
9
14
10
84,94;
108,18;
0; 0; 10,99
74,97
19,78
Из данных таблицы видно, что метод регуляризации Тихонова дал
о т риц а т е л ьный результат — в решении присутствует значитель-
ный относительный вклад атомного реактора (которого нет в истинном
решении). В методах многокритериального программирования (квадра-

















