
Н.М. Гордеева
2
на подобласти, найти решения для каждой подобласти и затем их
совместить. Геометрию течения в донной области можно определить,
если предположить, что струйный пограничный слой тонок и разме-
ры области течения сжатия малы. Тогда полное давление на критиче-
ской линии тока восстанавливается в задней критической точке и
становится равным статическому давлению за хвостовым скачком
(рассчитанному по параметрам невязкого течения). Использовав эту
модель, Чэпмен нашел решение для профилей скорости в отрывном
струйном пограничном слое. Это решение справедливо, если отрыв-
ной струйный пограничный слой не имеет начальной толщины или
если его длина достаточно велика и влияние начального распределе-
ния скорости пренебрежимо мало.
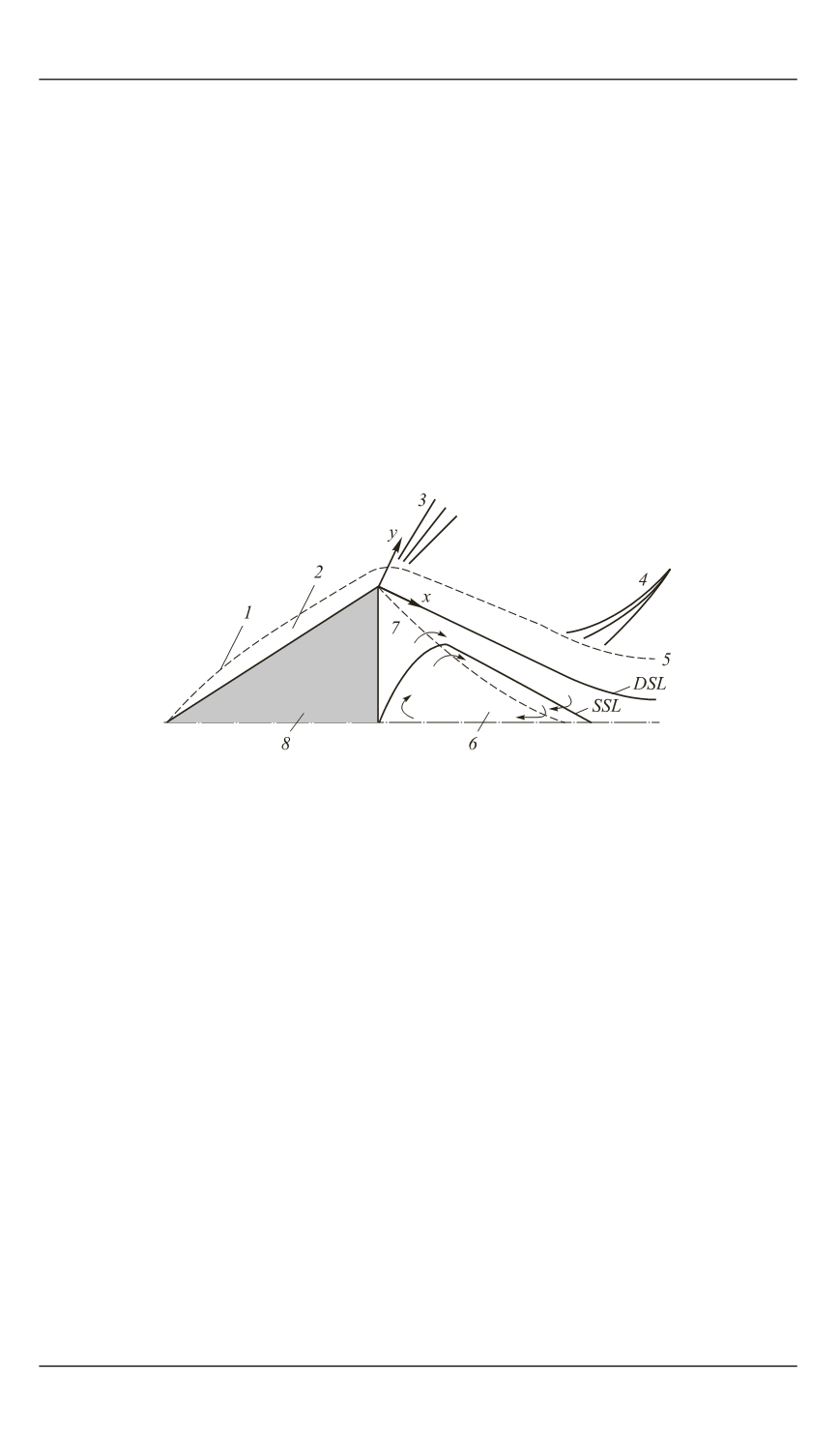
Рис. 1.
Схема течения в донной области:
DSL
— разделяющая линия тока;
SSL
— критическая ли-
ния тока;
1 —
скачок уплотнения;
2 —
пограничный слой;
3
— веер разрежения;
4
— хвостовой скачок;
5
— граница
«горла»;
6
— зона циркуляционного течения;
7
— зона энерго-
массообмена;
8
— осесимметричное тело
В работах [1, 5] представлены расчеты неавтомодельного отрыв-
ного струйного пограничного слоя методом конечных разностей в
рамках модели Чэпмена с начальным распределением скоростей, со-
ответствующим профилю Блазиуса. Используя некоторые предполо-
жения относительно профиля энтальпии, этот метод можно приме-
нить для определения параметров течения в донных областях за ко-
нусами и клиньями. В результате расчетов найдено, что длина
струйного пограничного слоя от тела до «горла» слишком мала для
того, чтобы установилось «чэпменовское» асимптотическое распре-
деление скоростей поперек слоя. Эти результаты позволяют расши-
рить метод анализа и включить в него расчет профилей полной эн-
тальпии [1–3]. Предполагается, что число Льюиса и число Прандтля

















