Некоторые соотношения дискретного и волнового в динамических системах
5
На рис. 2 представлена пятая форма собственных колебаний с ча-
стотой 459 с
–1
и периодом 0,0137 с, являющаяся результатом инте-
грирования системы дифференциальных уравнений (1).
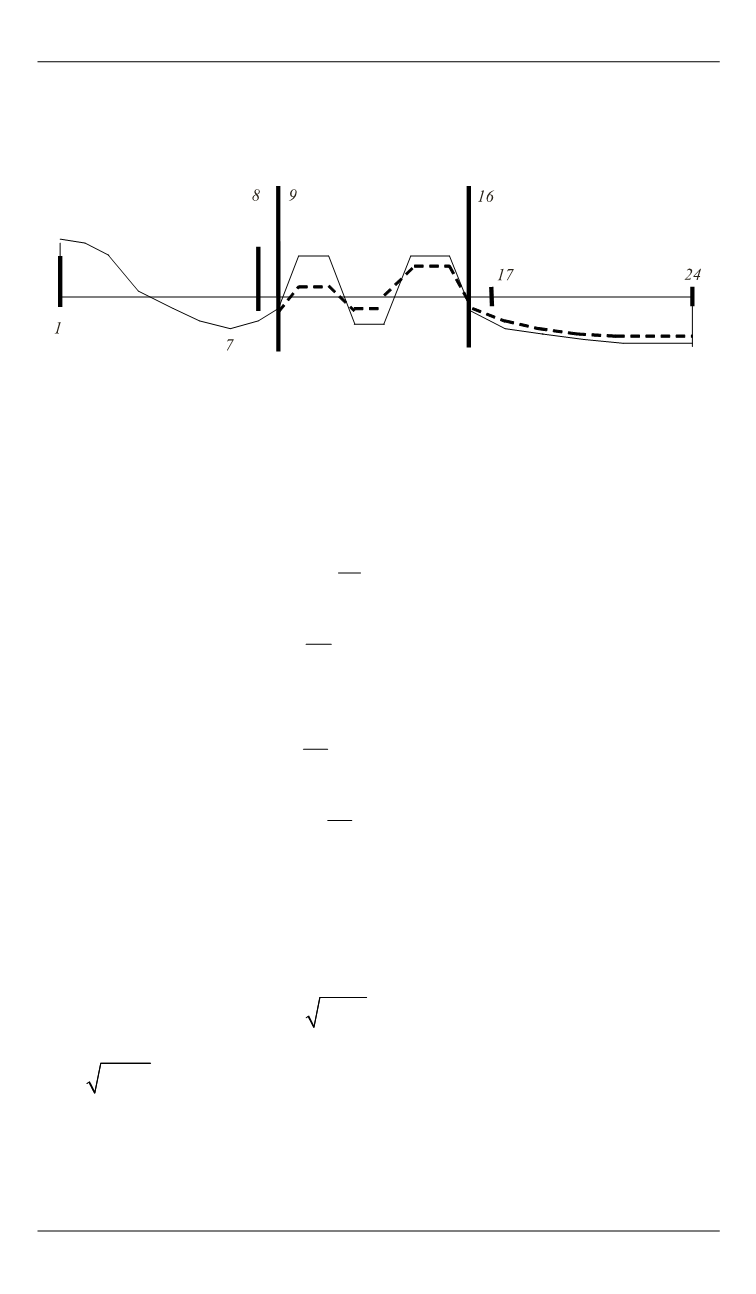
Рис. 2.
Собственная форма 24-массовой динамической системы
Однако если источник энергии расположен в первой массе, а по-
тери энергии сосредоточены на последней массе, то будут преобла-
дать волновые свойства системы и, следовательно, дифференциаль-
ные уравнения (1) станут некоторым аналогом волнового уравнения:
1
1 2
1
(
)
2
;
c
J
9
8
9 10
2
(
2
);
c
J
… (2)
17
16
17 18
3
(
2
);
c
J
24
23
24
3
.
(
2 )
c
J
В уравнениях (2) отношение
с
/
J
представляет собой аналог фазо-
вой скорости, а выражение в скобках — разностный аналог второй
производной.
Анализируя эту динамическую систему как волновую, получаем,
что в первой части рассматриваемой системы за половину периода
при фазовой скорости
1
1
/
v c J
= 1042 уч./с бегущая волна прохо-
дит семь масс, во второй части системы с фазовой скоростью
2
2
/
v c J
= 328 уч./с за период волна проходит 4,5 массы. Таким
образом, используя волновые характеристики, можно получить соб-
ственные частоты и формы колебаний.
Волновые особенности дискретных динамических систем вносят
в форму бегущей волны существенные изменения. Так, на стыке


