Некоторые соотношения дискретного и волнового в динамических системах
3
Следовательно, возникает вопрос о взаимосвязи между коллек-
тивным движением материальных точек и движением каждой от-
дельной частицы в волне. Нобелевский лауреат М. Борн пишет:
«Волна представляет собой состояние движения частиц, а не движе-
ние частиц самих по себе» [2]. Академик Л.И. Седов, рассматривая
распространение синусоидальных волн, пишет: «Если параметры
волны постоянные, то волна распространяется вдоль направления
движения как твердое тело» [3]. С.Э. Хайкин отождествляет бегущую
волну с движением точек струны, находящейся в абсолютно твердой
трубке, изогнутой и виде синусоиды и движущейся с постоянной
скоростью вдоль струны [4]. Движение тех точек струны, которые
находятся внутри трубки, будет точно таким же, как и при распро-
странении по струне бегущей волны. Л.Д. Ландау проводит аналогию
между волновым процессом и механикой материальных частиц, по-
лагая, что волновой вектор волны в распространении волн играет
роль импульса частицы в механике, а частота — роль энергии части-
цы [5].
Особенности поведения отдельной точки и коллективного дви-
жения точек в волне можно проиллюстрировать на известном приме-
ре движения двух волн, бегущих в противоположные стороны. На
рис. 1,
а
показаны несколько фаз распространения начального откло-
нения, заданного в виде равнобедренного треугольника. Эту форму
получают, если оттянуть струну в середине отрезка длиной
l
на высо-
ту
h
, придерживая ее в концах отрезка.
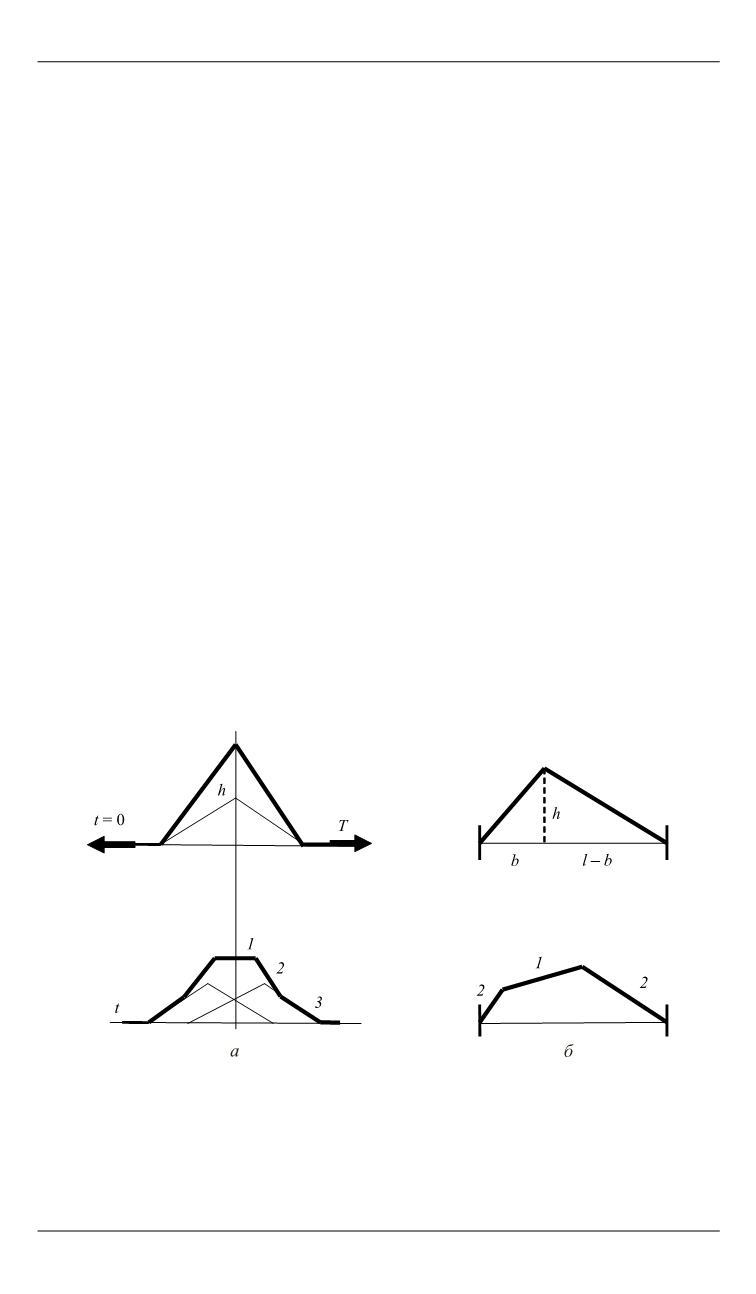
Рис. 1.
Формы струны в различные моменты времени
При отпускании верхней точки образуются две бегущие волны с
максимальным отклонением
h
/2, распространяющиеся в противопо-
ложных направлениях со скоростью
v
. Создающаяся при этом стоячая


