П.Г. Русанов
4
Для вывода уравнений динамики рассматриваемой механической
системы относительно инерциальной системы отсчета
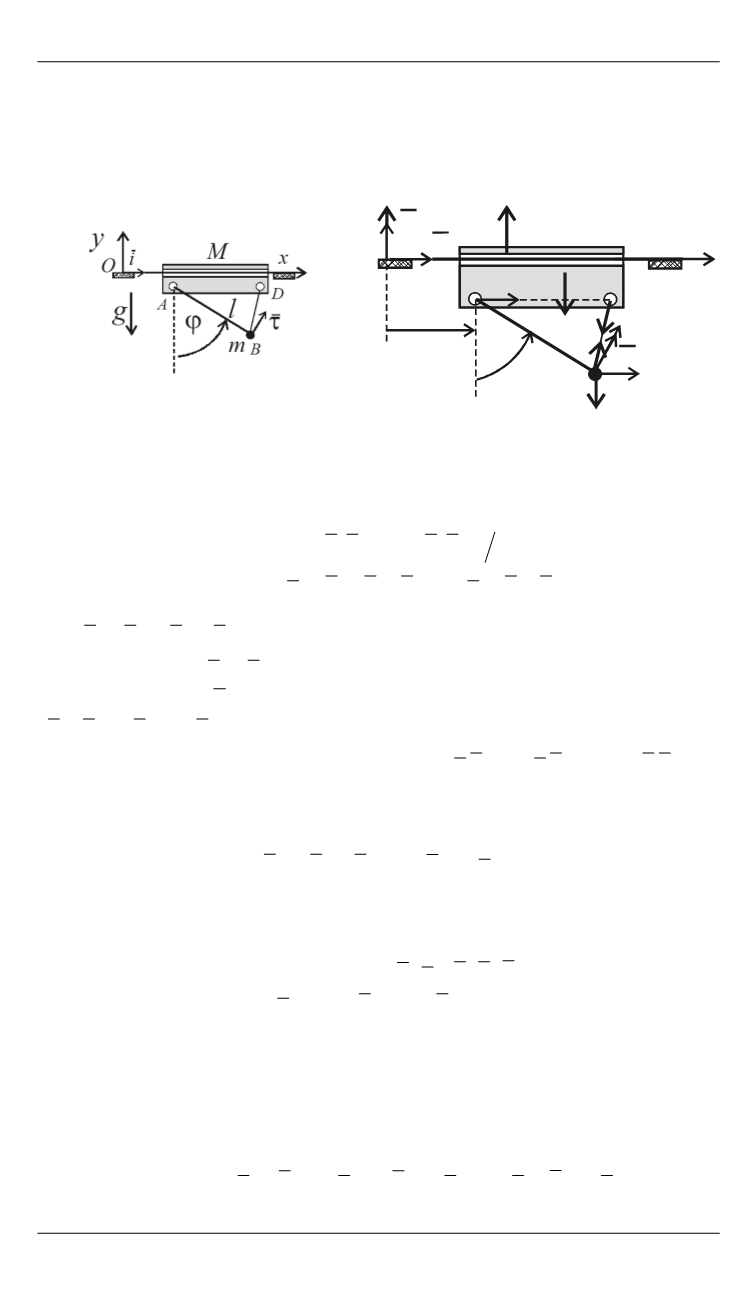
Оxyz
(рис. 2),
жестко связанной с основанием, применим алгоритм (3), основанный
на теореме (1).
l
i
j
y
x
x
x
A
B
D
O
N
V
V
V
B
F
F
mg
Mg
x
D
l
Рис. 1.
Схема механизма, совершаю-
щего плоскопараллельное движение
Рис. 2.
Силовое кинематическое
состояние механической системы
Для рассматриваемой консервативной системы тел
,
(
)
(
) 2;
,
A A
B B
e i
D A
B B
T M V V m V V
W M g N F V mg F V
(6)
где
A
V
,
B A BA
V V V
— векторы скоростей точек
A
и
B
относительно
системы
Оxyz
;
,
M g mg
— векторы сил тяжести ползуна и материаль-
ной точки
В
;
N
— сила воздействия основания на ползун;
,
, (
)
B D D
B
F F F F
— силы воздействия нити на ползун и матери-
альную точку
В
, причем произведения
,
0
A
A
M gV mgV
и
0
A
NV
тождественно равны нулю.
Представим скорость точки
В
в виде
,
B A BA x
V V V V i V
(7)
где
,
x
V x V s
априори являются независимыми проекциями векто-
ров переносной и относительной скоростей для точки
В
на соответ-
ствующие касательные направления
, ;
i
, ,
i j k
— орты декартовой
систем координат
Оxyz
;
cos
sin
i
j
— орт естественной систе-
мы координат в точке
В
, касательный к дуге окружности с центром в
точке
А
и радиусом
АВ
=
l
, лежащей в плоскости
Оxy
; s — криволиней-
ная координата положения точки
B
, причем угол
/
s l
представляет
собой угол отклонения стержня
АВ
от вертикали.
Тогда
,
0.
e i
A x
B x
B
T W M a V i
ma V i V mg F V


