В.В. Лапшин, Е.А. Юрин
6
С учетом формулы (1) коэффициент восстановления
1
1
d
k
d
.
(12)
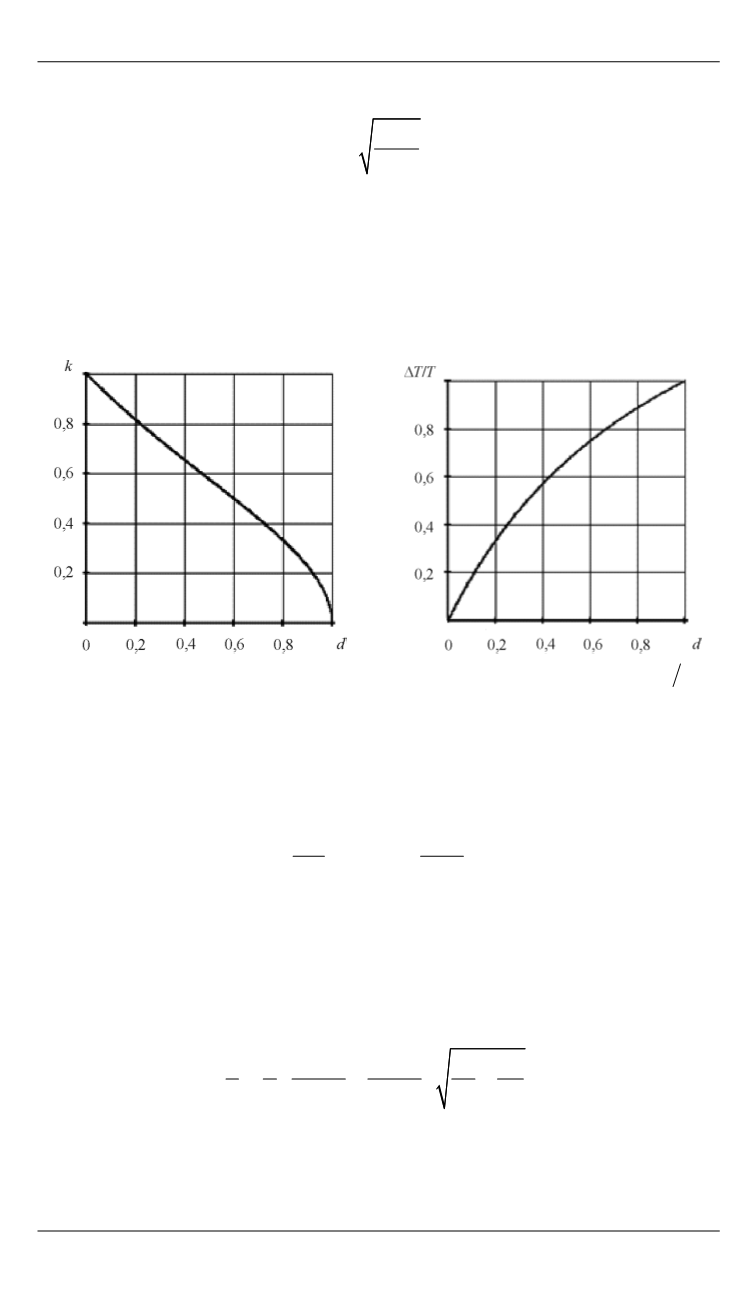
График зависимости коэффициента восстановления от постоян-
ной сухого трения
d
приведен на рис. 2. С ростом
d
коэффициент
восстановления монотонно убывает и становится равным нулю при
1
d
(т. е. удар становится абсолютно неупругим). При этом коэф-
фициент восстановления не зависит от скорости соударения, что про-
тиворечит экспериментальным данным [1, 10].
Рис. 2.
Зависимость коэффициента восстановления
k
и отношения
T T
от постоянной сухого трения
d
Кинетическая энергия, потерянная при ударе
,
T
определяется
соотношением (2). Обозначим через
T
кинетическую энергию тела
до удара, тогда
2
2
1
1
T
d
k
d
T
и зависит только от постоянной сухого трения (см. рис. 2).
Результаты математического моделирования.
Если поверхно-
сти тела и препятствия в окрестности точки соприкосновения сфери-
ческие, то сила упругой деформации в соответствии с результатами
[4, 5] имеет вид
3/2
( )
.
f x cx
Здесь
2
2
1
2
1
2
1 2
1 3 1
1
1 1 ,
4
с
E E R R
где
1, 2
E
— модули упругости;
1,2
— коэффициенты Пуассона;
1, 2
R
—
радиусы поверхности тела и препятствия.


