В.В. Лапшин, Е.А. Юрин
4
при ударе, является сухим. Контактная сила взаимодействия тела и
препятствия определяется соотношением
( , )
( )
( ) sgn ,
F F x x f x d f x x
(2)
где
x
— перемещение тела в процессе удара (деформации);
( )
f x
—
упругая сила взаимодействия тел при ударе;
d
— постоянная сухого
трения.
В процессе удара деформация
0,
x
в начале и в конце удара
0
x
. Упругая сила взаимодействия тел при ударе равна нулю в
начале и в конце удара:
(0) 0
f
и является возрастающей функцией
деформации
.
x
С учетом уравнения (2) уравнение движения тела в фазе дефор-
мации (при
0
V x
) имеет вид
( , )
( )(1 ),
mx F x x f x d
(3)
где
m
— масса тела.
В конце фазы деформации скорость движения
0.
V x
Если
постоянная сухого трения
1,
d
то в конце фазы деформации тело
останавливается. Контактная сила взаимодействия равна нулю. Удар
является абсолютно неупругим.
Если
1,
d
то удар является упругим и в фазе восстановления
(при
0
V x
) уравнение движения имеет вид
( , )
( )(1 ).
mx F x x f x d
(4)
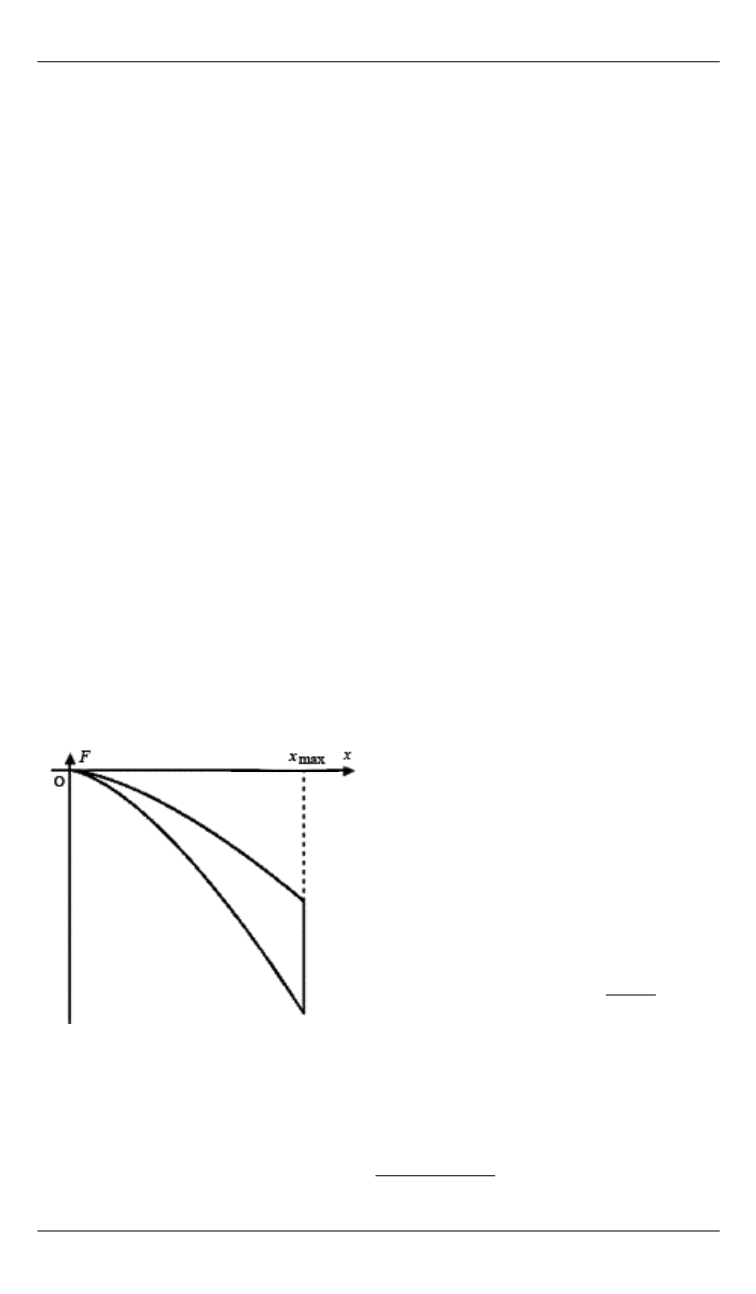
Зависимость контактной силы
от деформации в случае упругого
удара приведена на рис. 1.
Обозначим через
( )
x
— по-
тенциальную энергию упругой
деформации, тогда
0
( )
( ) ,
x
x f x dx
в частности
1
( )
1
n
cx x
n
при
( )
.
n
f x cx
Уравнения движения (3)–(4)
имеют первые интегралы — инте-
гралы энергии. В фазе деформации
2
2
2(1 ) ( )
( )
,
d x
V V
m
(5)
Рис. 1.
Зависимость контактной силы
от деформации при упругом ударе


