Математическое моделирование отрывного дозвукового обтекания…
5
Граничное условие непротекания, записанное в форме (4), в
совокупности с граничными условиями затухания возмущений на
бесконечности дало возможность заключить, что потенциал
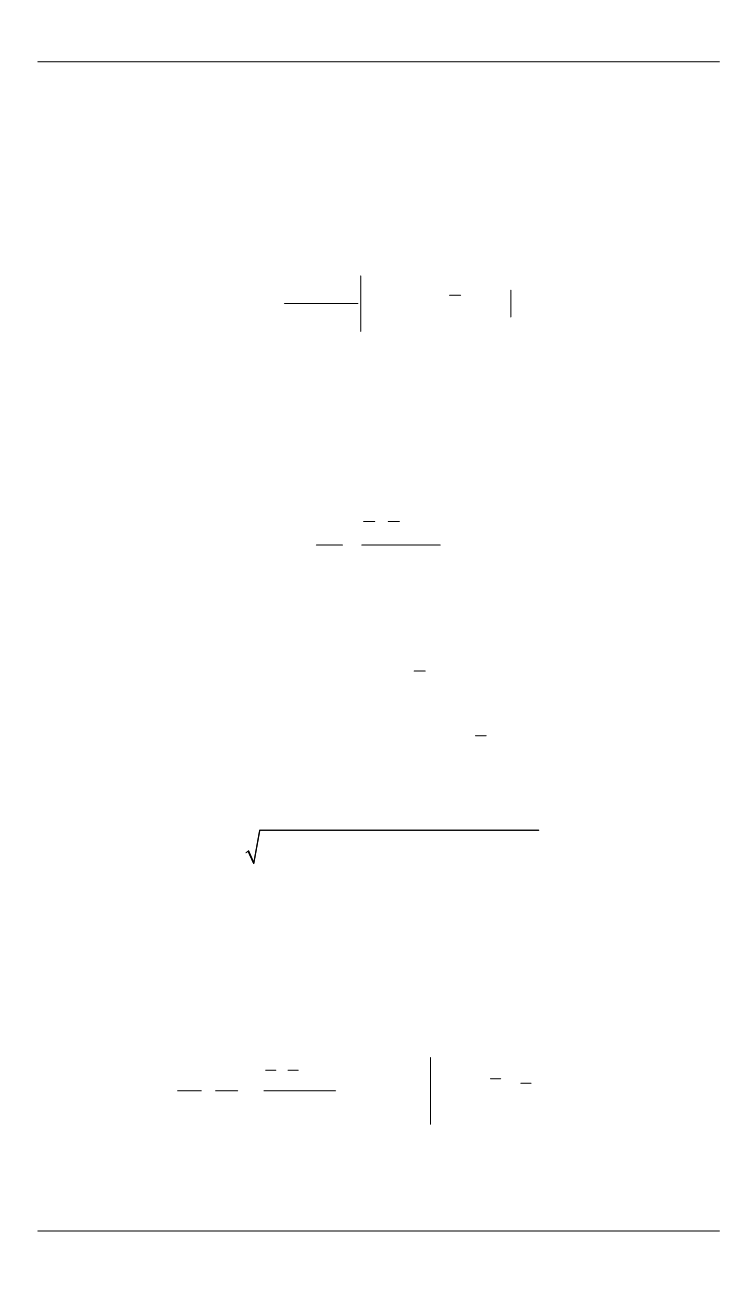
возмущенных скоростей
0
( )
M
должен являться решением внешней
задачи Неймана для уравнения Лапласа:
0
(
0);
M
(5)
0
0
( )
( ) ;
M V n M
n
(6)
0
0
( ) 0,
;
M M
(7)
0
0
( ) 0,
.
M M
(8)
Внешняя задача Неймана имеет единственное решение, которое
представляется в виде потенциала двойного слоя:
0
3
1
( )
( )
( )
4
r n M
M
g M d
r
, (9)
где
0 0 0 0
( , , )
M x y z
точка, в которой вычисляются потенциал
воз-
мущенных скоростей и скорость потока;
( , , )
M x y z
точка, распо-
ложенная на элементе площади
;
d
( )
n M
орт вектора нормали
к поверхности
,
проведенный в точке
;
M
( )
g M
поверхност-
ная плотность потенциала двойного слоя;
r
вектор, направлен-
ный из точки
M
в точку
0
;
M
r
модуль указанного вектора, вы-
числяемый по формуле
2
2
2
0
0
0
(
) (
) (
) .
r
x x
y y
z z
Потенциал двойного слоя (9) является решением уравнения
Лапласа (5) и удовлетворяет граничным условиям (7), (8) затухания
возмущений на бесконечности. Граничное условие непротекания
(6) будет выполнено и потенциал двойного слоя станет решением
внешней задачи Неймана, если поверхностная плотность
) (
Mg
бу-
дет решением интегрального уравнения [6]:
0
0
3
1
( ) ( )
( ),
4
M
r n M g M d
V n M
n
r


