В.Н. Тимофеев
10
сят от длины
сл
l
задней части эквивалентного тела во всем исследо-
ванном диапазоне изменения этого параметра
сл
2 ...4
l
d d
.
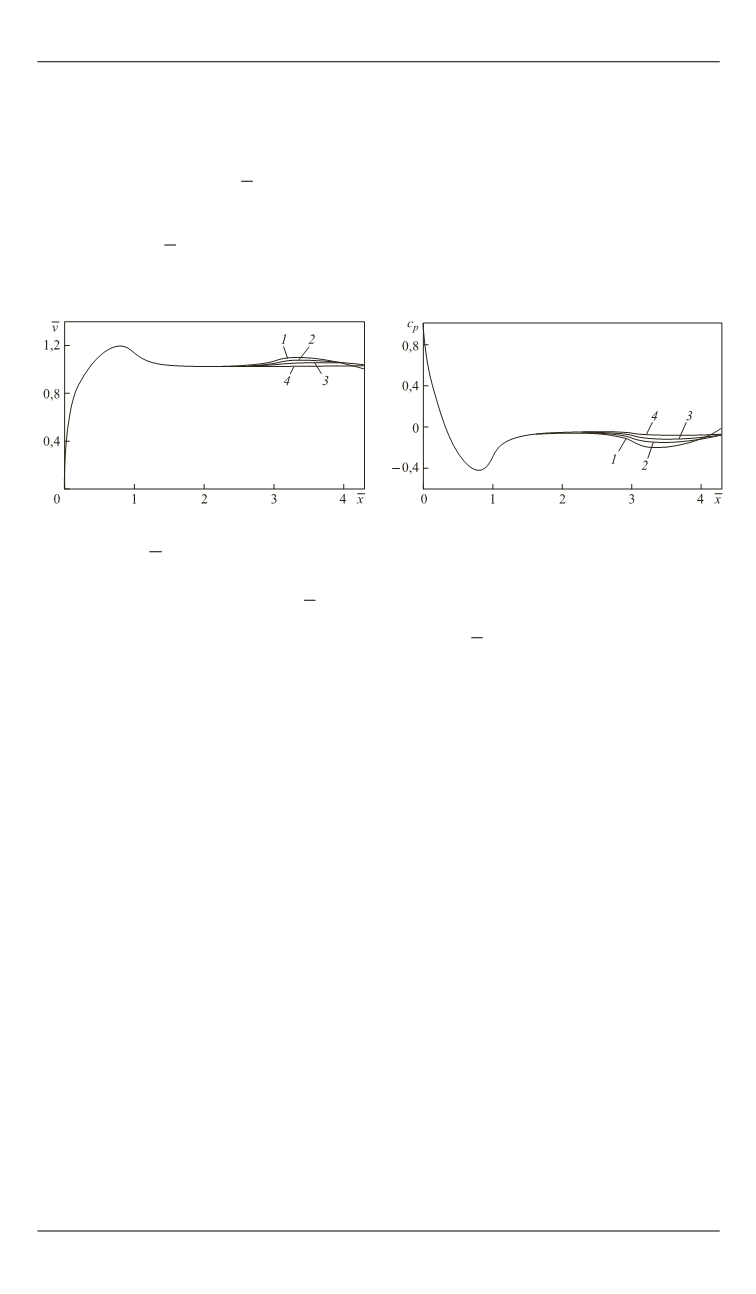
На рис. 2 и 3 представлены зависимости соответственно безраз-
мерной скорости
/
v v V
и коэффициента давления
p
c
на
поверхности эквивалентного тела от безразмерной продольной
координаты
/
x x d
и длины
сл
l
хвостового участка эквивалентного
тела.
Рис. 2.
Зависимость безразмерной
скорости
v
на поверхности экви-
валентного тела от безразмерной
продольной координаты
x
и
длины
сл
l
хвостового участка
эквивалентного тела:
сл
2
l
d
(
1
); 2,5
d
(
2
); 3
d
(
3
); 4
d
(
4
)
Рис. 3.
Распределение коэф-
фициента давления
p
c
по обра-
зующей эквивалентного тела от
безразмерной продольной коор-
динаты
x
и длины
сл
l
хвостового
участка эквивалентного тела:
сл
2
l
d
(
1
); 2,5
d
(
2
); 3
d
(
3
); 4
d
(
4
)
Было установлено, что если длина хвостового участка эквива-
лентного тела превышает 3,5
d
, то влияние параметра
сл
l
на распре-
деление коэффициента давления проявляется лишь в окрестности
донного среза.
В ряде случаев, например при нахождении силы лобового сопро-
тивления, должно быть учтено донное давление, которое зависит от
формы и геометрических параметров обтекаемого тела и от режимов
течения в пограничном слое (от числа Рейнольдса). Определение
донного давления и расчетным и экспериментальным путем
до-
вольно сложная задача.
Предлагаемая методика моделирования станет полностью
замкнутой, если удастся определить длину
сл
l
поверхности
2
задней части эквивалентного тела.
Первоначально (см. [2]) с этой целью были использованы экспе-
риментальные данные, представленные в работе [9]. Для фюзеляжей
с плоским донным срезом при числе Рейнольдса
6
5 10
путем отбра-


