Моделирование процесса взаимодействия ударной волны…
7
В этом случае, если
1 2 ,
n
g
решение при
0
совпадает с
асимптотическим и дает качественно верное решение при
,
так
как
удовлетворяет соответствующему предельному переходу при
0
s
в поле изображений.
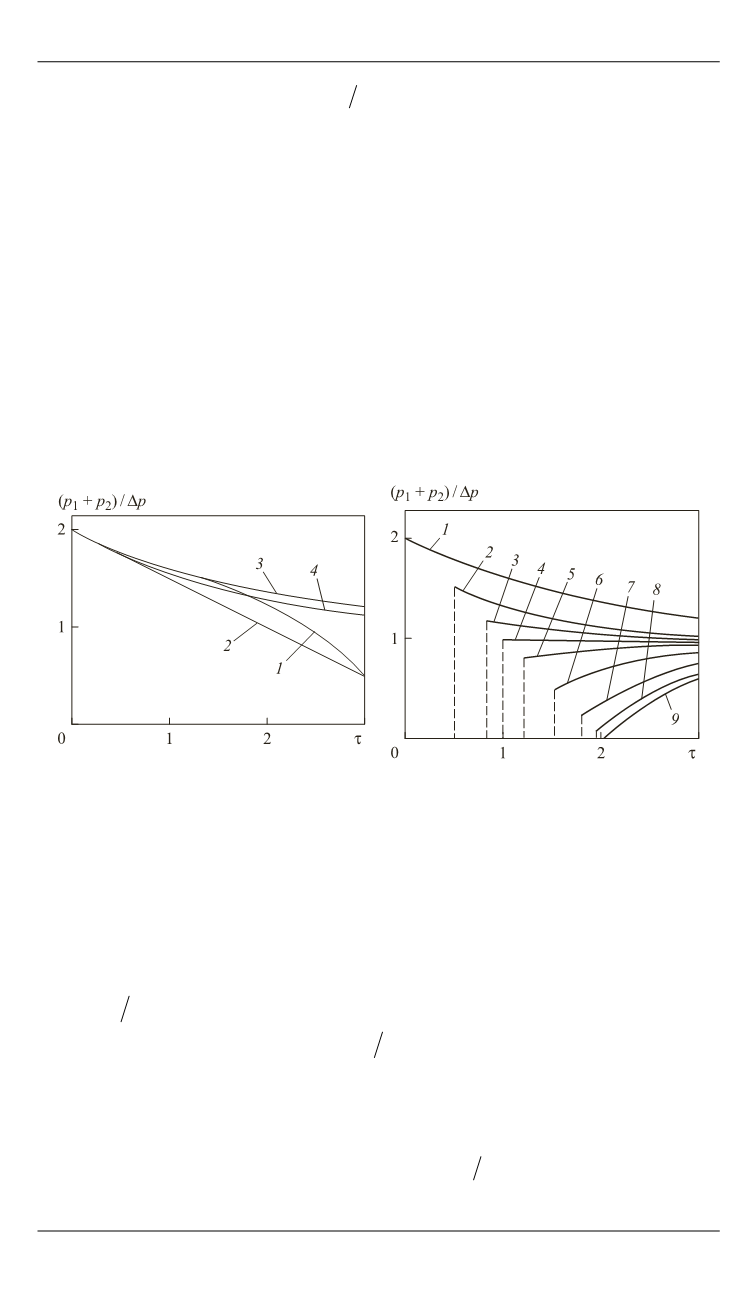
На рис. 3 приведены зависимости давления во фронтальной точке
0
оболочке от параметра
,
полученные с помощью асимпто-
тической (7) и приближенной (9) формул. Для сравнения также при-
ведена кривая, соответствующая известному решения Блейха [10].
Как следует из рисунка, при
< 2,0 оба решения практически совпа-
дают, после чего начинается их расхождение. При
> 2,0 можно
импользовать только формулу (7).
Аналогично можно найти давление в любой точке цилиндриче-
ской поверхности. На рис. 4 приведены значения давления для раз-
личных участков цилиндрической оболочки.
Рис 3.
Зависимость давления во фрон-
тальной точке оболочки от безразмер-
ного момента времени:
1
— точное решение;
2
— решение при
сохранении двух членов разложения;
3
— приближенное решение;
4
—
приближенное решение Блейха
Рис 4.
Зависимость давления в различ-
ных точках оболочки от безразмерного
параметра времени:
0
(
1
); 60
(
2
); 80
(
3
); 90 (
4
); 100 (
5
);
120 (
6
); 140 (
7
); 160 (
8
); 180
(
9
)
Полученные результаты справедливы для слабых ударных волн, ко-
гда
ф 0
0,3,
p р
где
0
р
— давление в невозмущенной среде перед
фронтом ударной волны. При
ф 0
0,3
p р
полученное давление сле-
дует умножить на коэффициент
отр
.
K
На основании этих результатов
можно представить следующую картину изменения давления на по-
верхности оболочки. При достижении фронтом ударной волны любой
точки передней поверхности оболочки
2
давление в ней мгно-
венно возрастает до максимального значения
p
=
p
1
+
p
2
, а затем падает


