Л.В. Северова, C.П. Северов
4
корпуса аппарата как твердого тела на одном листе фазовой биплос-
кости в координатах
1
( ),
( )
k
k
n
x
t y
t
, а на другом листе в ко-
ординатах
1
,
n
n n
x
y
отобразим относительное движение ап-
парата — дополнительные угловые колебания корпуса, вызываемые
поперечными колебаниями упругих ВЭ. Перепишем (2) в виде
( ) ,
.
n
n
dy
dx y
dt
dt
(4)
Разделив первое уравнение на второе и проинтегрировав при
0
(0)
x
x
,
0
(0)
x
x
, получим уравнение фазовой траектории пере-
носного движения
2 2
0
0
2
2 ( ) (
).
n
y y
x x
(5)
Решение (3) с учетом
2
1
n
имеет вид
2
cos(
)
( ) / .
n n
t
n
n
n
e A
t
k
(6)
Обозначив
2
1
( ) / ,
c n
n
n
k
c
A
, запишем (6) в виде
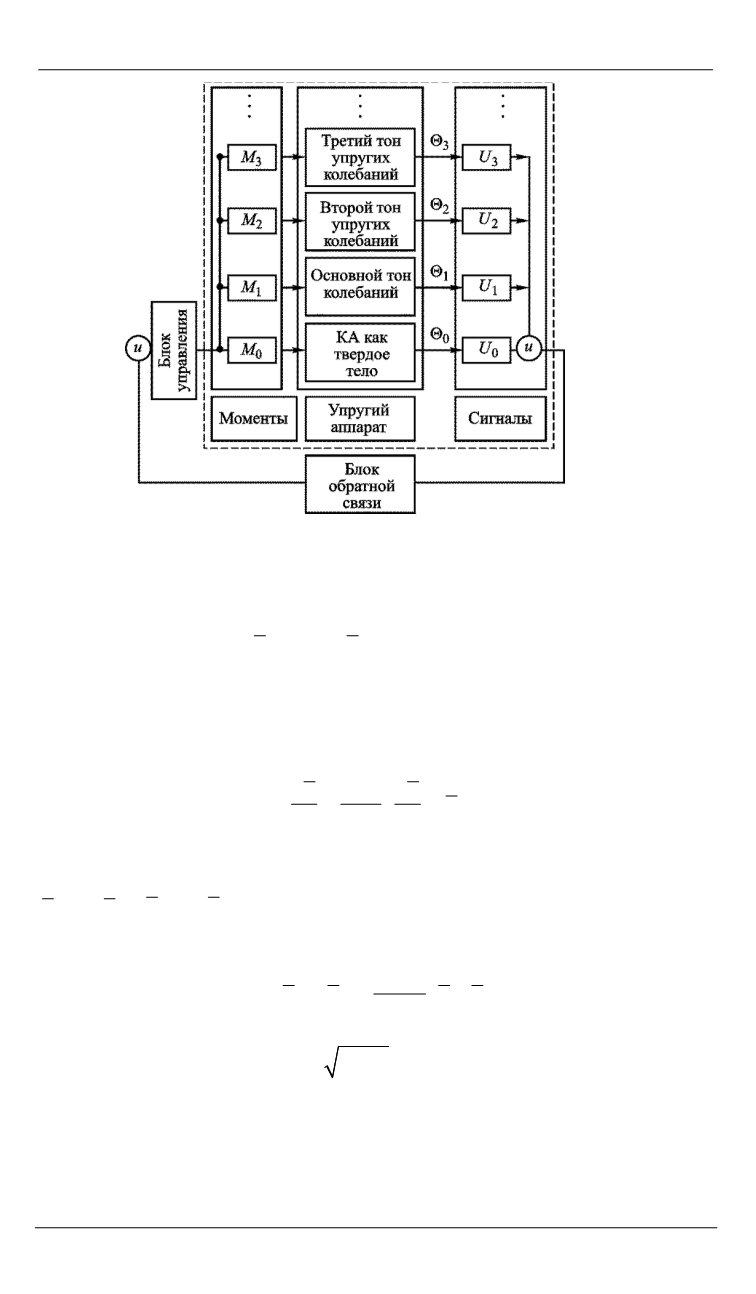
Рис. 1


