О.Д. Алгазин, А.В. Копаев
6
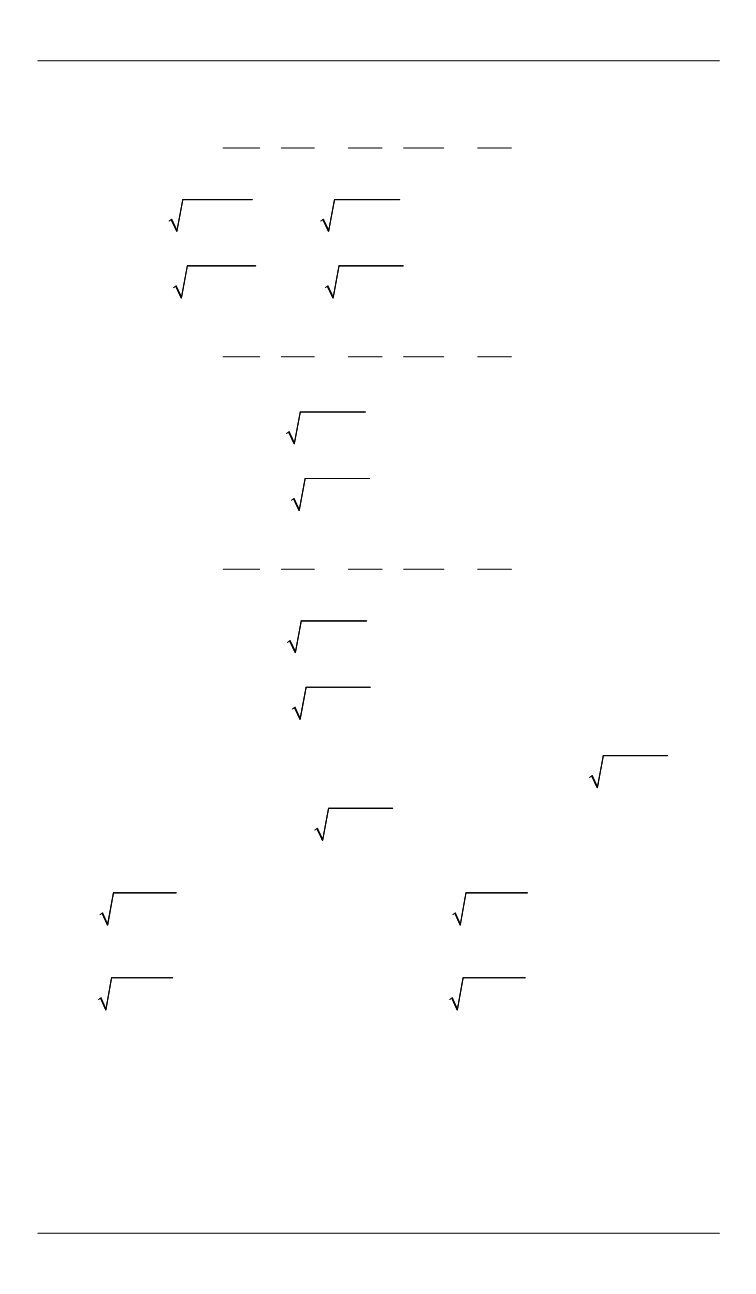
Действительно,
2
2
1
12
1
P
p
x x
x x
x
∂ϕ ∂ ∂ϕ ∂
∂ϕ
= + γ = + γ =
∂ ∂
∂ ∂
∂
(
)
2 2
2 2
1
2
1 2
1 2
exp
cos ( ) cos ( )
x
y
z
= − λ + λ ⋅
− λ +λ ⋅
λ
λ −
(
)
2 2
2 2
1
1
1 1
1 1
exp
cos ( ) cos ( );
x
y
z
− γ λ + λ ⋅
− λ +λ ⋅
λ
λ
2
2
1
12
1
P
p
y y
y y
y
∂ϕ ∂ ∂ϕ ∂
∂ϕ
= + γ = + γ =
∂ ∂
∂ ∂
∂
(
)
2 2
1
1
2
1 2
exp
sin ( ) cos ( )
x
y
z
= −λ − λ +λ ⋅
λ
λ −
(
)
2 2
1
1
1
1 1
exp
sin ( ) cos ( );
x
y
z
− γλ − λ +λ ⋅
λ
λ
2
2
1
12
1
P
p
z
z
z
z
z
∂ϕ ∂
∂ϕ ∂
∂ϕ
= + γ = + γ =
∂ ∂
∂ ∂
∂
(
)
2 2
2
1
2
1 2
exp
cos ( ) sin ( )
x
y
z
= −λ − λ +λ ⋅
λ
λ −
(
)
2 2
1
1
1
1 1
exp
cos ( ) sin ( ).
x
y
z
− γλ − λ +λ ⋅
λ
λ
Поэтому, если
2
/ 0,
x
∂ϕ ∂ ≡
то функции
(
)
2 2
1 2
exp
x
− λ +λ ⋅ ×
1
2
cos ( ) cos ( )
y
z
× λ
λ
и
(
)
2 2
1
1
1 1
exp
cos ( ) cos ( )
x
y
z
− λ +λ ⋅
λ
λ
линейно за-
висимы, что неверно. Аналогично, если
2
/ 0,
y
∂ϕ ∂ ≡
то функции
(
)
2 2
1
2
1 2
exp
sin ( ) cos ( )
x
y
z
− λ +λ ⋅
λ
λ
и
(
)
2 2
1
1
1 1
exp
sin ( ) cos ( )
x
y
z
− λ +λ ⋅
λ
λ
линейно зависимы, что также неверно. Если
2
/ 0,
z
∂ϕ ∂ ≡
то функции
(
)
2 2
1
2
1 2
exp
cos ( )sin ( )
x
y
z
− λ +λ ⋅
λ
λ
и
(
)
2 2
1
1
1 1
exp
cos ( )sin ( )
x
y
z
− λ +λ ⋅
λ
λ
линейно зависимы, что также неверно. Отсюда следует, что
2
[ ] 0.
G
D
ϕ ≠
Продолжим этот процесс «ортогонализации»:
(
)
(
)
(
)
(
)
1 1
2 2
; ;
; ;
; ;
; ;
m
m
x y z P x y z
x y z
x y z
ϕ
=
+ γ ϕ
+ γ ϕ
+…+
(
)
1 1
; ; .
m m
x y z
− −
+γ ϕ


