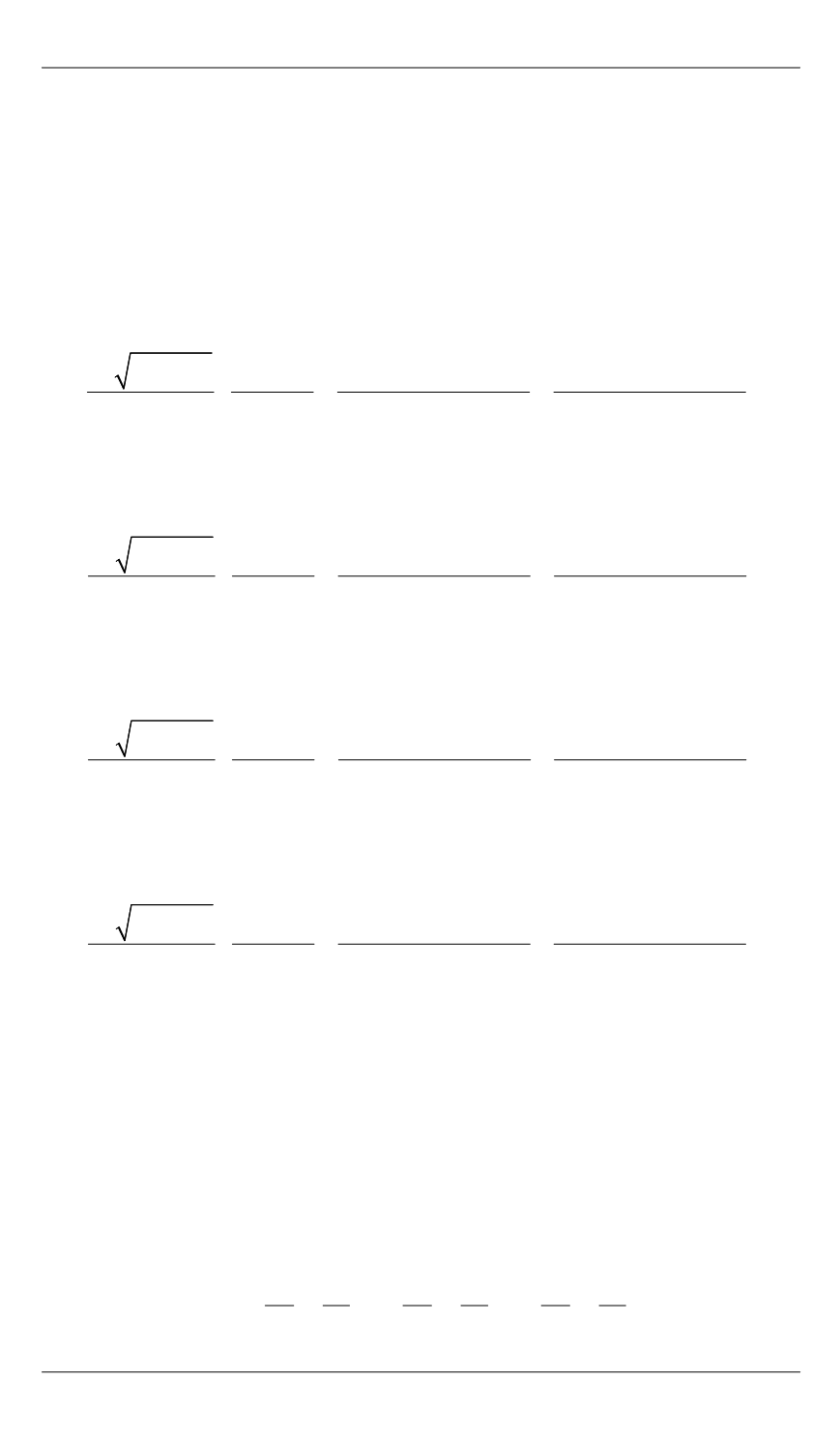
Приближение в четырехгранном угле гармонических функций трех переменных
3
(
) (
)
(
)
(
)
,
,
1 1
; ;
; ;
; ;
; ;
n n
m l m l
m l m l
m l
r x y z u x y z
a p x y z b q x y z
= =
=
−
+
+
⎡⎣
∑ ∑
(
)
(
)
,
,
; ;
; ;
.
m l m l
m l m l
c s x y z d t
x y z
+
+
⎤⎦
Непосредственным расчетом находим, что
(
)
,
; ;
G m l
D p x y z
⎡
⎤
=
⎣
⎦
(
)
(
)
2 2
2
2
2
2
2
2
2
2
2 2
2
2 2
1
;
2
1
1
m
m
l
l
m l
m
m
l
l
k
k
k
⎧
⎫
λ + λ
λ
λ
⎪
⎪
=
+
+
⎨
⎬
λ + λ
⎡
⎤ ⎡
⎤
⎪
⎪
λ + + λ
λ + + λ
⎣
⎦ ⎣
⎦
⎩
⎭
(
)
,
; ;
G m l
D q x y z
⎡
⎤
=
⎣
⎦
(
)
(
)
2 2
2
2
2
2
2
2
2
2
2 2
2
2 2
1
;
2
1
1
m
m
l
l
m l
m
m
l
l
k
k
k
⎧
⎫
λ + λ
λ
λ
⎪
⎪
=
−
+
⎨
⎬
λ + λ
⎡
⎤ ⎡
⎤
⎪
⎪
λ + + λ
λ + + λ
⎣
⎦ ⎣
⎦
⎩
⎭
(
)
,
; ;
G m l
D s x y z
⎡
⎤
=
⎣
⎦
(
)
(
)
2 2
2
2
2
2
2
2
2
2
2 2
2
2 2
1
;
2
1
1
m
m
l
l
m l
m
m
l
l
k
k
k
⎧
⎫
λ + λ
λ
λ
⎪
⎪
=
+
−
⎨
⎬
λ + λ
⎡
⎤ ⎡
⎤
⎪
⎪
λ + + λ
λ + + λ
⎣
⎦ ⎣
⎦
⎩
⎭
(
)
,
; ;
G m l
D t
x y z
⎡
⎤
=
⎣
⎦
(
)
(
)
2 2
2
2
2
2
2
2
2
2
2 2
2
2 2
1
;
2
1
1
m
m
l
l
m l
m
m
l
l
k
k
k
⎧
⎫
λ + λ
λ
λ
⎪
⎪
=
−
−
⎨
⎬
λ + λ
⎡
⎤ ⎡
⎤
⎪
⎪
λ + + λ
λ + + λ
⎣
⎦ ⎣
⎦
⎩
⎭
[
]
,
,
;
0,
G m l
m l
D p q
′ ′
=
[
]
,
,
;
0,
G m l m l
D p s
′ ′
=
[
]
,
,
;
0,
G m l m l
D p t
′ ′
=
[
]
,
,
;
0,
G m l m l
D q s
′ ′
=
[
]
,
,
;
0,
G m l m l
D q t
′ ′
=
[
]
,
,
;
0,
G m l m l
D s t
′ ′
=
, , ,
1, 2, , .
m l m l
n
′ ′ = …
Интеграл Дирихле для пары функций
(
)
; ;
u x y z
и
(
)
; ;
v x y z
опре-
деляется формулой [4]
[ ]
;
.
G
G
u v
u v
u v
D u v
dx dy dz
x x
y y
z z
⎡
⎤
∂ ∂
∂ ∂
∂ ∂
⎛ ⎞ ⎛ ⎞
⎛ ⎞ ⎛ ⎞
⎛ ⎞ ⎛ ⎞
=
+
+
⎢
⎥
⎜ ⎟ ⎜ ⎟
⎜ ⎟ ⎜ ⎟
⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠
⎝ ⎠ ⎝ ⎠
⎝ ⎠ ⎝ ⎠
∂ ∂
∂ ∂
∂ ∂
⎢
⎥
⎣
⎦
∫∫∫


