А.А. Пожалостин, Б.Г. Кулешов, А.В. Паншина
2
в классическом учебнике С.П. Тимошенко [8]. В этой модели сухое
трение не зависит от скорости скольжения элементов колебательной
системы.
Основные допущения состоят в следующем:
1) сухое трение считается небольшим;
2) предполагается, что формы собственных колебаний не изме-
няются при учете трения.
Известно, что последнее условие используют при расчете коле-
баний механических систем с малым вязким сопротивлением, а так-
же гидроупругости. Предполагается, что колебания малые, материал
подчиняется закону Гука, однороден, депланация сечений стержня
отсутствует, справедлива гипотеза сплошности среды.
Продольные колебания однородной консольной балки.
Для
построения методики расчета был использован метод приведенных
(эквивалентных) параметров и энергетический метод. Для вынуж-
денных колебаний систем с одной степенью свободы энергетический
метод применен С.П. Тимошенко [8].
Проиллюстрируем разработанную методику расчета на примере
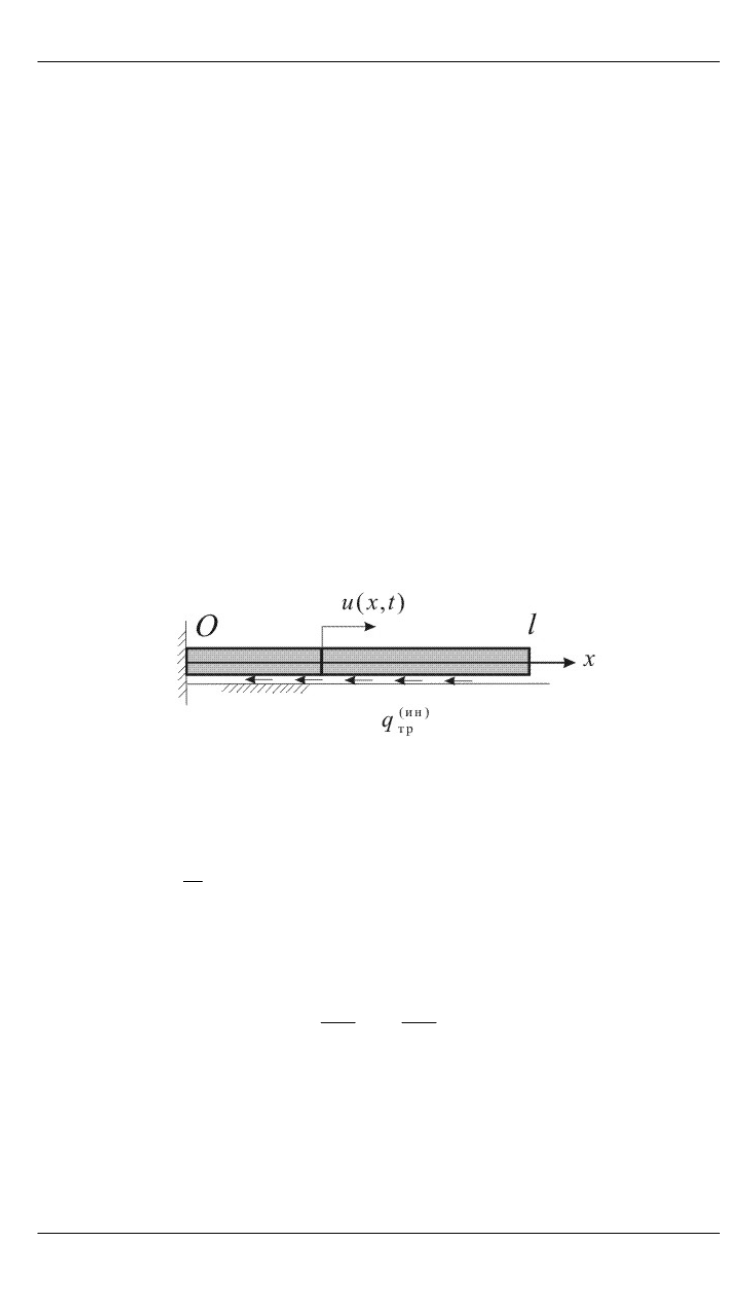
продольных колебаний однородной консольной балки (рис. 1).
Рис. 1.
Однородная консольная балка
Случай 1. Свободные колебания.
Предположим, что на балку
действует равномерно распределенная сила сухого трения интенсив-
ностью
(ин)
тр
,
G q
l
= δ
где
G
— сила тяжести стержня;
l
— его длина,
δ
— коэффициент кулонова трения 1-го рода.
Дифференциальное уравнение продольных колебаний имеет вид
[8–13]
2
2
0
0
2
2
0,
u
u
EF
x
t
∂
∂
− μ =
∂
∂
(1)
где
0
μ
— погонная масса;
0
EF
— жесткость стержня в продольном
направлении.
Частное решение уравнения (1), согласно методу Фурье [8, 11],
представим в виде


