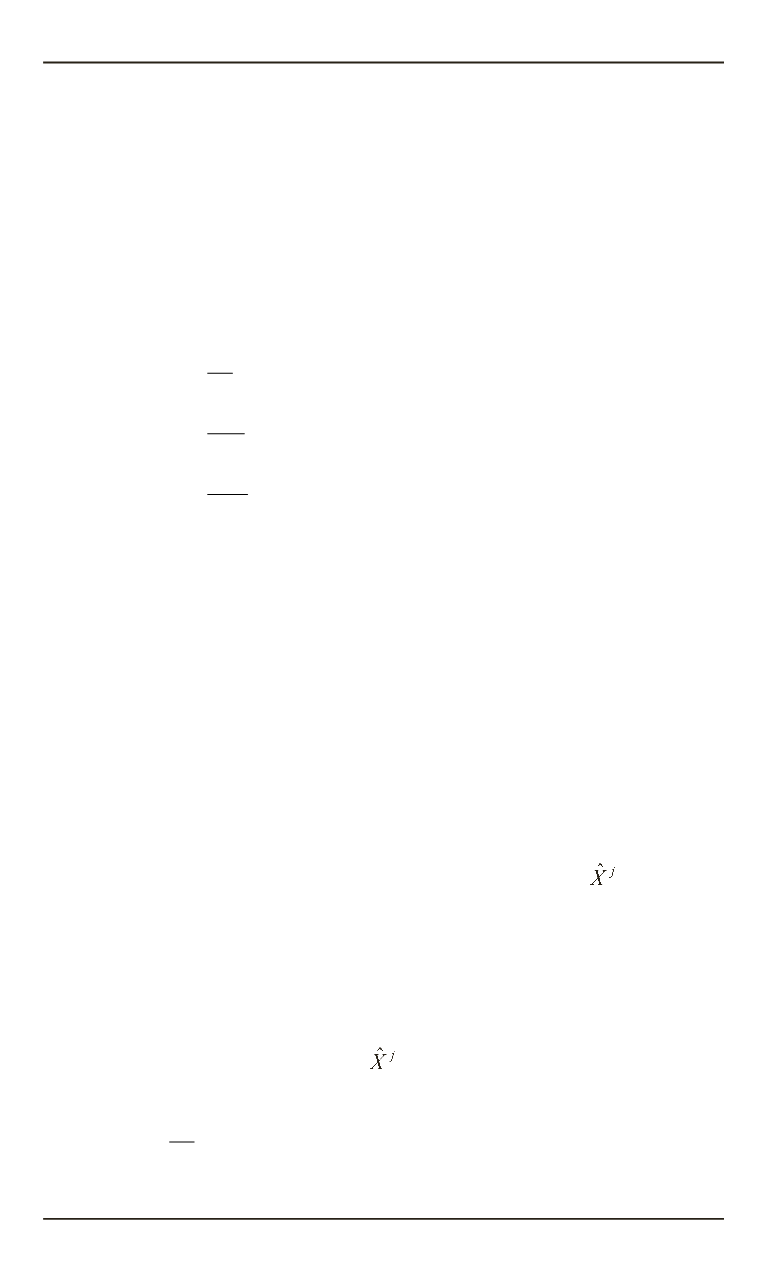
5
Комплексное моделирование движения ЛА и процессов горения в двигателях
Рассмотрим модель мгновенного сгорания твердого топлива [7–9],
в которой топливо, сгорая, сразу переходит в газовую фазу, состоя-
щую из продуктов сгорания, образование к-фазы учитывать не будем.
Движение продуктов сгорания в камере сгорания рассматривается
в рамках системы уравнений динамики идеального нетеплопроводно-
го газа, состоящей из уравнения неразрывности, уравнений движения и
уравнения энергии. Записанная в бескоординатной форме, эта система
уравнений в неподвижной системе координат, связанной с поверхно-
стью горения твердого топлива, имеет следующий вид [5]:
(
)
(
)
(
)
0,
0,
0,
t
p
t
E
E
E p
t
∂ρ⎧ + ⋅∇ρ + ∇ ⋅ ρ =
⎪ ∂⎪
∂ρ⎪ + ⋅∇⊗ρ + ∇ ⋅ ρ ⊗ + =
⎨ ∂⎪
∂ρ⎪ + ⋅∇ρ + ∇ ⋅ ρ + =
⎪ ∂⎩
c
v
v c
v
v v E
c
v
(7)
p
=
R
ρ
θ,
e
=
c
v
θ,
E
=
e
+ |
v
|
2
/2.
Здесь ρ — плотность газа;
t
— время;
E
— полная энергия газа;
e
—
внутренняя энергия;
c
v
— теплоемкость при постоянном объеме; θ —
температура газа; |
v
|
2
=
v
i
v
i
— квадрат модуля скорости;
p
— давле-
ние;
R
— газовая постоянная (
R
=
/
μ
; μ — молекулярная масса газа;
— универсальная газовая постоянная);
E
— метрический тензор;
∇
— набла-оператор Гамильтона [10];
c
— вектор движения поверх-
ности горения.
Решение системы уравнений газодинамики (7) ищется в фиксиро-
ванной неподвижной области
V
(
t
), соответствующей начальной гео-
метрии рабочего тракта ДУ (камера сгорания с топливом и сопло).
Компоненты вектора
c
в подвижной системе координат , связанной
с поверхностью горения, вычисляются по формуле [5]
( )
1/2 2
3
1
,
j
j
c D P
α
α
=
⎛
⎞
= ⎜
⎟
⎜
⎟
⎝
⎠
∑
(8)
где
j
P
α
— компоненты якобиевой матрицы преобразования неподвиж-
ных координат
X
j
в подвижные . Скорость горения топлива
D
за-
висит от давления
p
продуктов сгорания на твердой поверхности горе-
ния:
0
0
p
D D
p
ν
⎛ ⎞
=
,
⎜ ⎟
⎝ ⎠
здесь
D
0
,
v
— характеристики топлива;
p
0
= 10
5
Па.
Вследствие неоднородности топлива его скорость горения является