Д.Е. Ефанов, Е.А. Микрин, М.Ш. Мисриханов, А.В. Филимонов
8
2
2
1
2
3
2
0
0
1 1 1
⎡ ⎤ξ
⎢ ⎥
⎡
⎤
⎡ ⎤
σ σ σ
ψ = ⎢ ⎥
⎢
⎥
⎢ ⎥
⎣ ⎦
⎣
⎦ ⎢ ⎥
ν⎢ ⎥ ⎣ ⎦
,
(16)
все множество решений которого очевидно имеет вид
2
2 3
2
3 1
2
1
2
⎡ ⎤ ⎡
⎤
ξ σ − σ
⎢ ⎥ ⎢
⎥
ψ = σ − σ μ
⎢ ⎥ ⎢
⎥
⎢ ⎥ ⎢
⎥
ν σ − σ
⎢ ⎥ ⎢
⎥
⎣ ⎦ ⎣
⎦
.
(17)
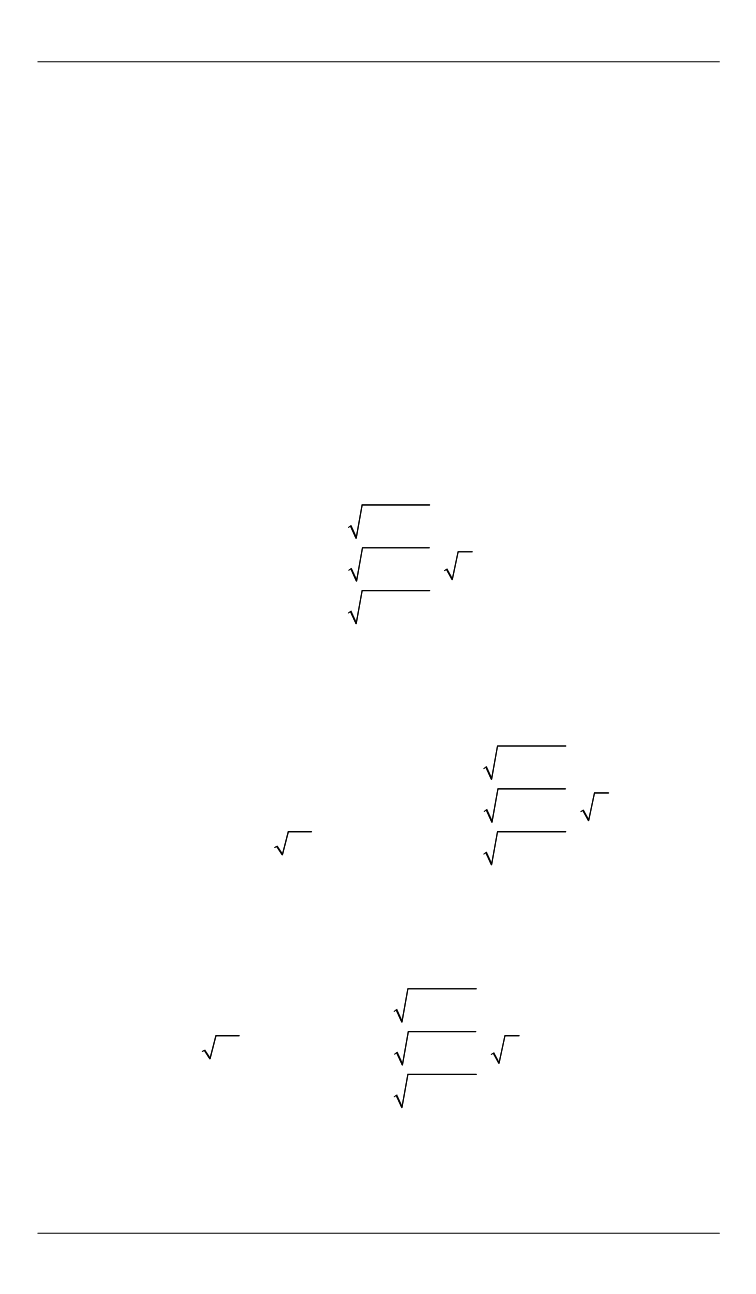
Искомые переменные вычислим путем поэлементного взятия
квадратного корня в виде
2 3
3 1
1
2
⎡
⎤
σ − σ
ξ⎡ ⎤ ⎢
⎥
⎢ ⎥ ⎢
⎥
ψ = σ − σ μ
⎢ ⎥ ⎢
⎥
⎢ ⎥ν ⎢
⎥
⎣ ⎦
σ − σ
⎣
⎦
.
(18)
Таким образом, решение в однородных координатах с учетом (11),
(14) и (18) имеет вид
2 3
11 12 13
21 22 23
3 1
31 32 33
1
2
0 0
0
0
0 0 1
a
u u u
b
u u u
u u u
⎡
⎤
σ − σ
⎡
⎤
α
⎡
⎤
⎡ ⎤
⎢
⎥
⎢
⎥ ⎢
⎥
⎢ ⎥
⎢
⎥
β =
σ − σ μ
⎢
⎥ ⎢
⎥
⎢ ⎥
⎢
⎥
⎢
⎥ ⎢
⎥
⎢ ⎥γ
⎢
⎥
−
⎣ ⎦
⎣
⎦ σ − σ
⎣
⎦
⎣
⎦
.
(19)
Перейдем из обобщенных координат в однородные, обеспечив тож-
дество
γ
= 1 из условия
[
]
2 3
31 32 33
3 1
1
2
1
1
u u u
⎡
⎤
σ − σ
⎢
⎥
⎢
⎥
−
σ − σ μ =
⎢
⎥
⎢
⎥
σ − σ
⎣
⎦
,
(20)
которое единственным образом определяет ограничение на свобод-
ную переменную


