Матричный метод преобразования прямоугольных геоцентрических координат…
3
использованием тригонометрических формул. Однако обратное пре-
образование, которое рассматривается в данной работе, осуществля-
ется значительно сложнее. В случае эллипсоида вращения исключе-
нием является вычисление долготы, для чего используют формулу,
имеющую замкнутый вид в исходных координатах.
Одно из возможных решений задачи преобразования координат
может быть получено путем определения проекции внешней точки
P
G
(
x
G
,
y
G
,
z
G
) на референцный эллипсоид по направлению нормали к
его поверхности
P
E
(
x
E
,
y
E
,
z
E
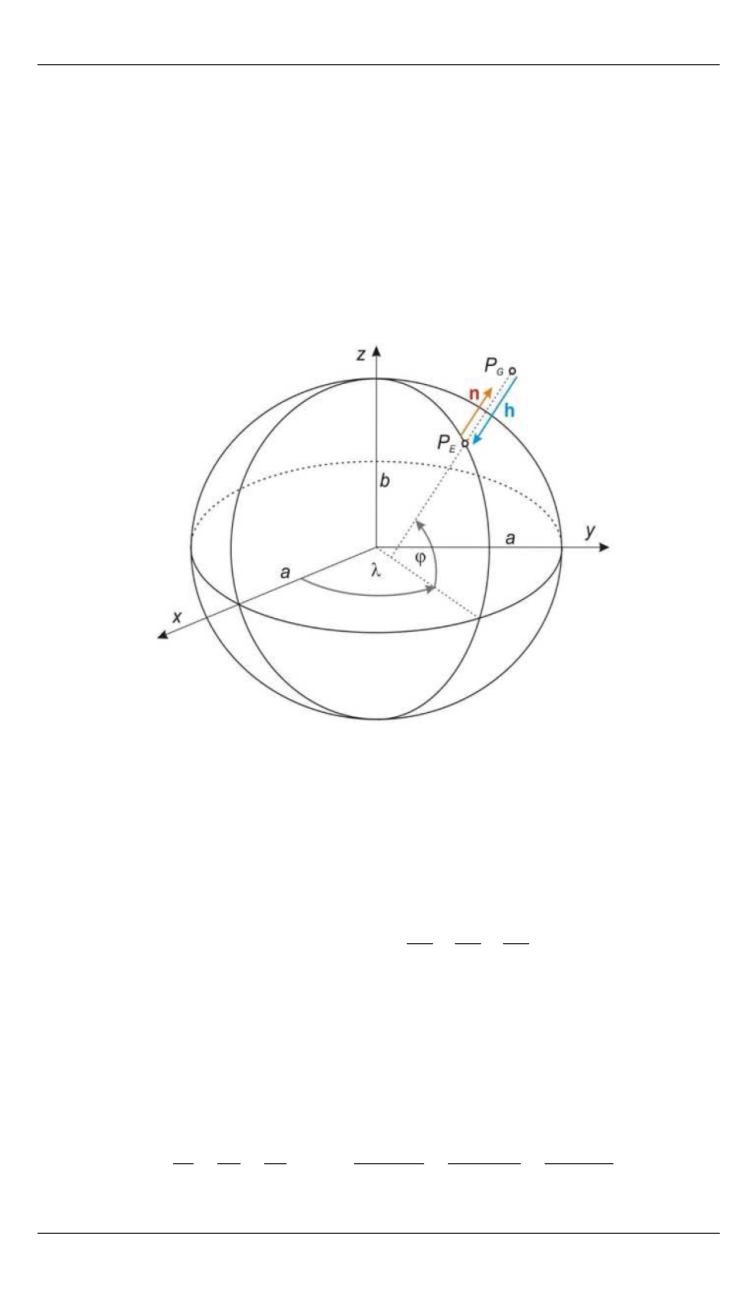
), как показано на рис. 1.
Рис. 1.
Проецирование точки на эллипсоид с помощью
коллинеарных векторов
n
и
h
Это можно сделать с помощью построения двух коллинеарных
векторов: вектора
n
, нормального к поверхности эллипсоида в точке
P
E
, определяемого с помощью градиентного оператора [6]
[
]
1 2 3
2
2
2
2
E E E
x x x
n n n n
a a a
⎡
⎤
=
= ⎢
⎥
⎣
⎦
,
и вектора
h
, соединяющего точки
P
G
и
P
E
,
[
] [
]
1 2 3
E G E G E G
h h h h x x y y z z
=
= −
−
−
.
Из теории векторных вычислений известно, что координаты колли-
неарных векторов пропорциональны с постоянным коэффициентом
k
:
3
1
2
2
2
2
1
2
3
E G E G E G
E
E
E
h
x x y y z z
h h
k
k
n n n
a x
a y
b z
−
−
−
−
−
−
= = = ⇒ =
=
=
.
(2)


