Д.Е. Ефанов, Е.А. Микрин, М.Ш. Мисриханов, А.В. Филимонов
4
Кроме того, координаты точки
P
E
должны удовлетворять уравне-
нию эллипсоида вращения:
2
2
2
2
2
2
1
E E E
x y z
a a b
+ + =
.
(3)
Совместное решение уравнений (2) и (3) является решением за-
дачи определения проекции точки на эллипсоид.
Несмотря на то что данный подход может быть применен и при
решении задачи преобразования координат для трехосного эллипсо-
ида [8], для эллипсоида вращения размерность задачи можно сокра-
тить путем приведения задачи к меридианному эллипсу как показано
на рис. 2 [6].
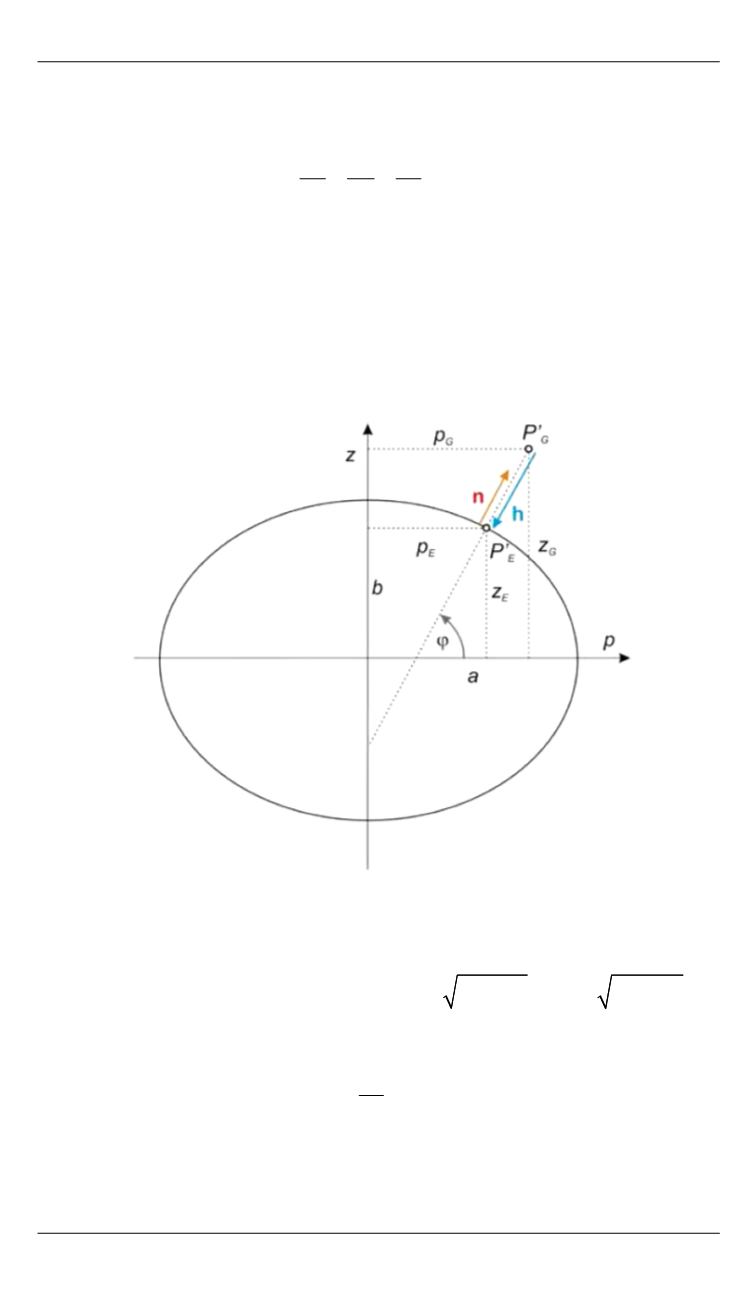
Рис. 2.
Приведение задачи преобразования координат
к меридианному эллипсу
Здесь
(
)
,
G
G G
P p z
=′
,
(
)
,
E
E E
P p z
=′
,
2
2
E
E E
p x y
= +
,
2
2
G G G
p x y
= +
и
2
2
cos ,
sin .
E
E
p N
b
z
N
a
= ϕ
⎧
⎪
⎨
=
ϕ
⎪⎩
(4)
В этом случае вектор
n
, нормальный к меридианному эллипсу в точке
E
P
′
, определяется в виде


