Н.Е. Зубов, А.В. Лапин, Е.А. Микрин
12
н
н
opt
н
н
н
1, 018exp 2, 071
0,849, если 0
85 ,
180
( )
2,177 exp 0, 726
0,155, если 85
180 ,
180
a
⎧
πϑ
⎛
⎞
−
−
−
< ϑ ≤ °
⎜
⎟
⎪
⎝
⎠
⎪
ϑ = ⎨
πϑ
⎛
⎞
⎪ −
−
−
° < ϑ ≤ °
⎜
⎟
⎪
⎝
⎠
⎩
(5.7)
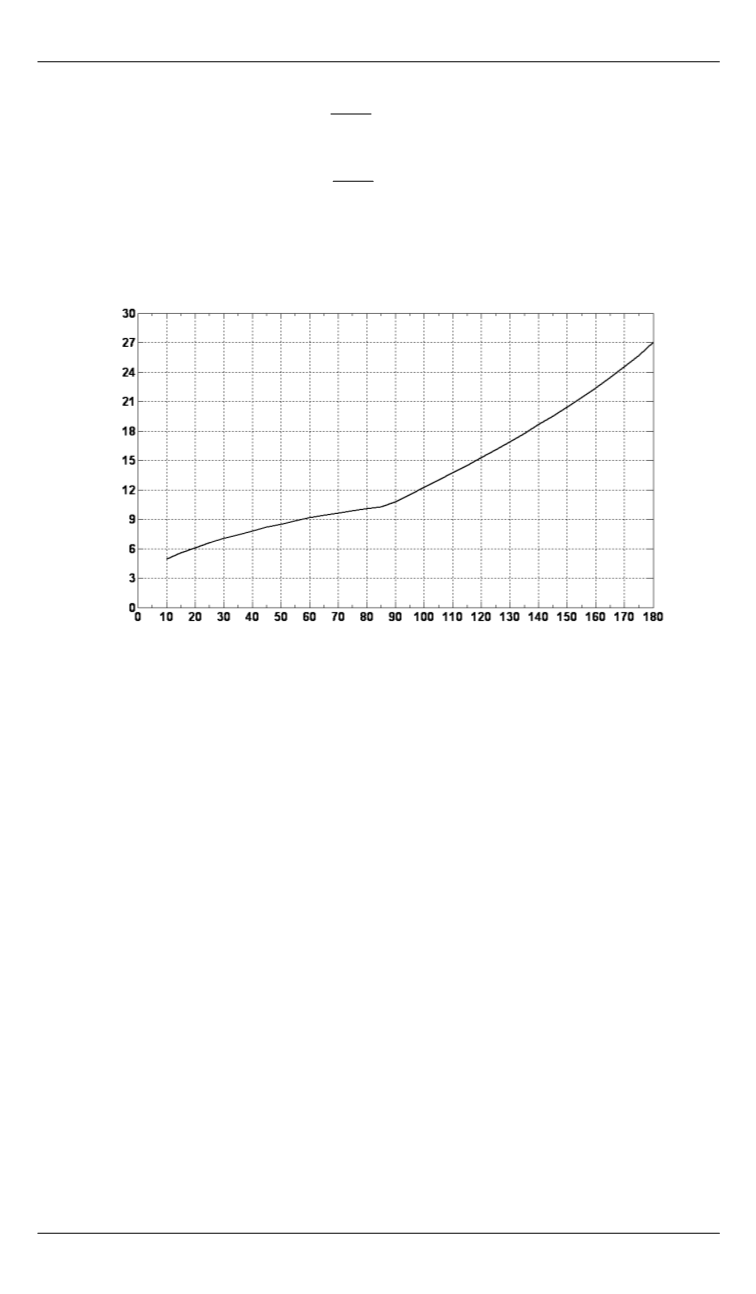
которую можно применять на практике. График этой зависимости
представлен на рис. 1 (приближение).
н
, град
ϑ
ПП min
, с
T
Рис. 2.
Минимальные значения времени ПП при различных
начальных условиях
6. Пример численного моделирования.
Рассматривается тот же,
что и в [9], пример численного моделирования для следующих
начальных условий:
λ
н1
= 0,3,
λ
н2
= –0,5,
λ
н3
= 0,8 (компоненты век-
торной части кватерниона),
ω
н1
= –10 град/с,
ω
н2
= –7 град/с,
ω
н3
=
= 11 град/с (компоненты вектора угловой скорости). Начальный угол
конечного поворота, таким образом, задан равным
ϑ
н
= 163,74°, чему,
согласно (5.7), соответствует значение параметра
a
= –0,428.
По результатам численного моделирования в среде Delphi были
построены графики ПП для компонент кватерниона (рис. 3) и для
компонент вектора угловой скорости (рис. 4).
Длительность ПП составила 22,8 с, что согласуется с проектными
требованиями, предъявляемыми ко времени работы посадочных дви-
гателей. Максимальное значение модуля угловой скорости оказалось
равным 28,3 град/с, а наибольшие значения градиентов угловой ско-
рости по каждому из каналов управления составили соответственно
2,1, 16,4 и 16,1 град/с. Таким образом, ПП удовлетворяет заданным
ограничениям (5.5).


