Количественный подход к прогнозированию светостойкости полимерных материалов …
7
Результаты и обсуждение.
Для решения системы интегральных
уравнений (4) был использован метод конечных сумм [8], когда инте-
гралы в этой системе вычислялись с помощью квадратурных формул
прямоугольников (шаг сетки 10 нм). В результате система (4) сведена
к системе линейных алгебраических уравнений (СЛАУ), решение
*
которой определялось с помощью метода наименьших квадратов и с
использованием малого параметра регуляризации по невязке в пра-
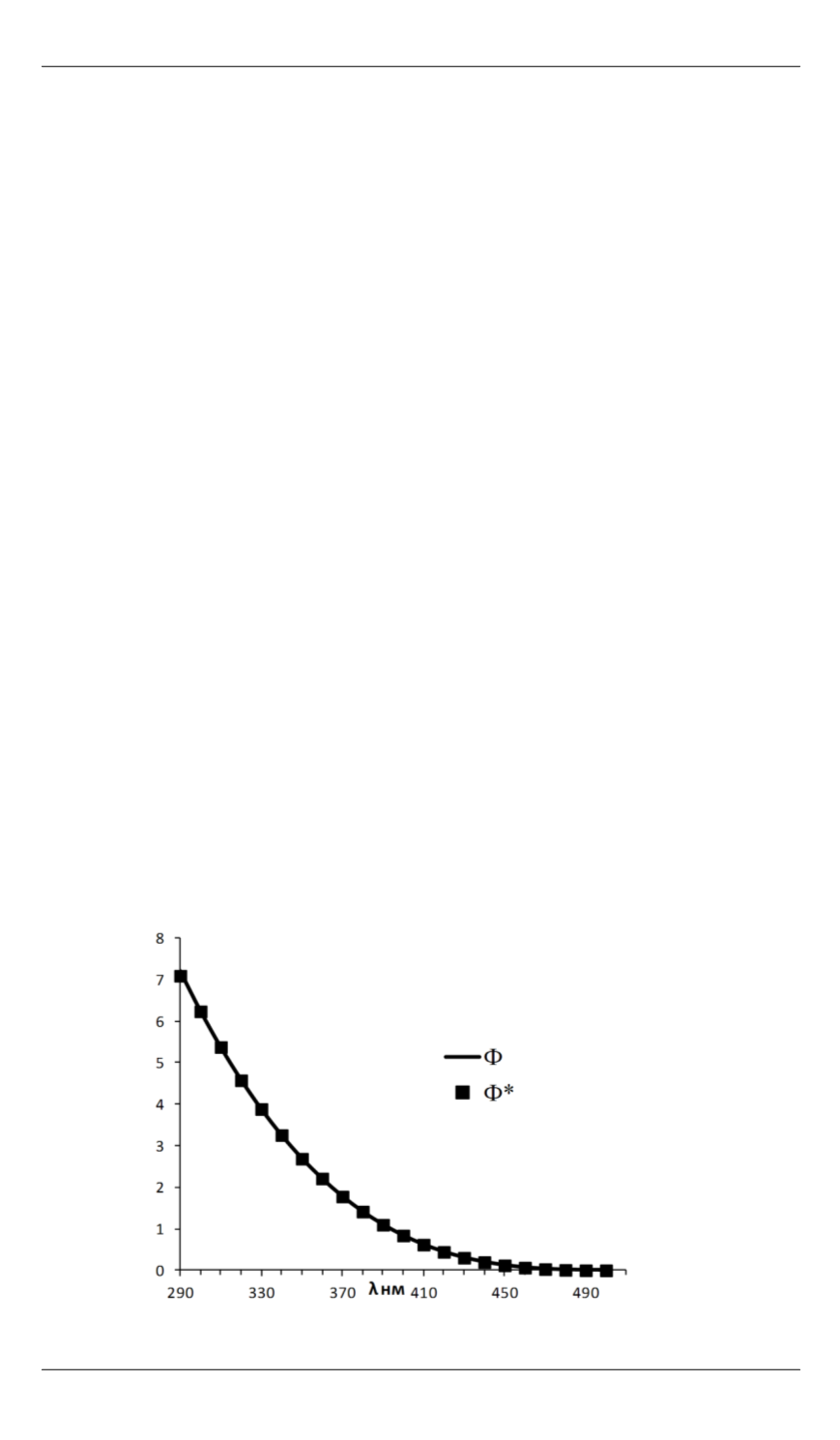
вой части системы интегральных уравнений (5). На рис. 2 показаны
графики модельного
(см. последний столбец в табл. 1) и рассчи-
танного
*
(согласно используемому регуляризированному методу
конечных сумм) квантовых выходов. Для количественного сравнения
квантовых выходов
и
*
в табл. 2 приведены их значения для
рассматриваемого в работе диапазона длин волн облучения. Сравне-
ние графиков зависимостей квантовых выходов
и
*
от длин волн
приведены на рис. 2. Кроме того, на рис. 3 (см. также табл. 2) показа-
ны графики интегральных показателей
и
*
квантовых выходов
и
*
соответственно, для которых
500
( )
( )
d
,
(7)
500
* ( )
* ( )
d
.
(8)
Интегралы в формулах (7) и (8) вычислены приближенно на ос-
нове квадратурных формул прямоугольников (шаг сетки 10 нм).
Рис 3.
Интегральные показатели
и *
квантовых выходов
и *


