Математическое моделирование температурного состояния пространственных. . .
Примеры расчета температурного состояния стержневых конст-
рукций.
Изложенная выше методика математического моделирования
нестационарного температурного состояния стержневых конструкций
реализована в виде комплекса прикладных программ, который при-
менялся для исследования ряда конструкций. При этом была учтена
возможность зависимости теплофизических свойств и параметров, ха-
рактеризующих граничные условия второго и третьего рода, от тем-
пературы.
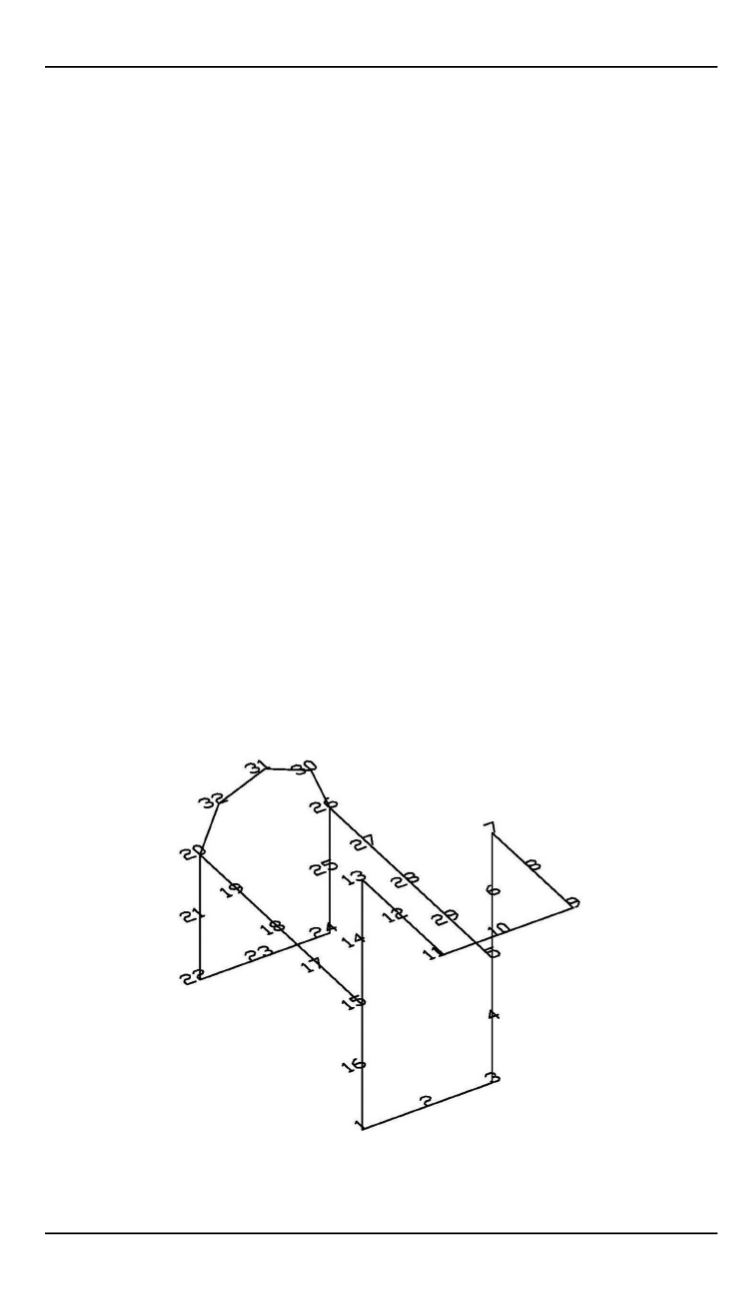
На рис. 2 показана исследуемая стержневая конструкция. В ка-
честве конечных элементов выбраны квадратичные трехузловые эле-
менты. Кроме того, на рис. 2 приведена глобальная нумерация узлов
соответствующей конечно-элементной модели. Конвективный тепло-
обмен осуществлялся на боковых поверхностях двух конечных эле-
ментов
1
и
2
:
1
— узлы 24, 25, 26;
2
— узлы 11, 12, 13. В зоне
1
= 900
K и
a
= 135
Вт
/
(
м
2
·
K
)
, а в зоне
2
= 500
K и
a
= 60
Вт
/
(
м
2
·
K
)
. Начальная температура принята равной
300
K.
Результаты расчетов представлены на рис. 3–5. Как следует из ри-
сунков, стержневая конструкция имеет неравномерное распределение
температуры. Заметно интенсивнее нагрев осуществляется в зоне узла
25, менее нагретыми являются удаленные участки (зоны узлов 3, 9).
Кроме того, усиливается влияние зоны наиболее интенсивного наг-
рева на зону менее интенсивного нагрева. На рис. 5 представлены
температурные поля в фиксированные моменты времени, показыва-
ющие кинетику роста общего температурного состояния стержневой
системы.
Рис. 2.
Глобальная нумерация узлов конечно-элементной модели
стержневой конструкции
9


