И.В. Станкевич
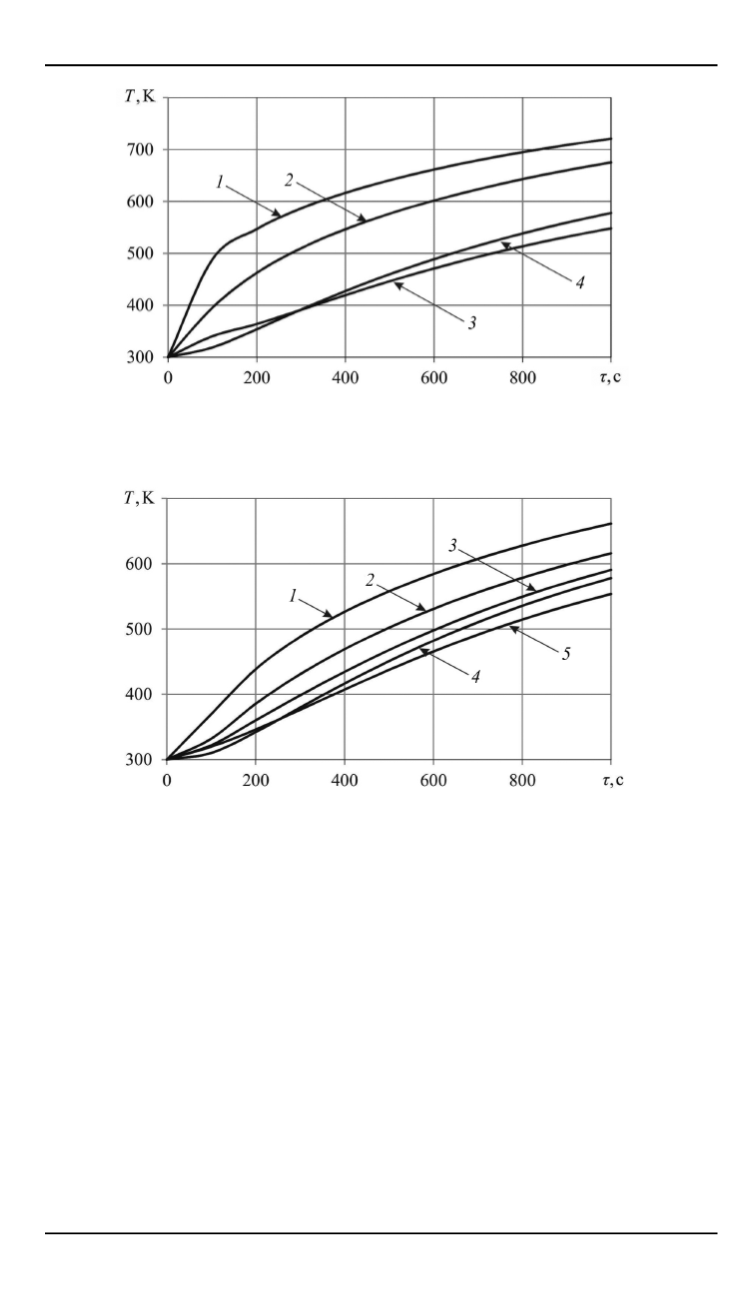
Рис. 3.
Изменение температуры узлов конечно-элементной модели: 25 (
1
), 31 (
2
),
12 (
3
), 15 (
4
)
Рис. 4.
Изменение температуры узлов конечно-элементной модели: 20 (
1
), 18 (
2
),
5 (
3
), 3 (
4
), 9 (
5
)
Выводы.
Рассмотрены особенности построения конечно-элемент-
ной технологии решения нестационарных и нелинейных температур-
ных задач применительно к пространственным стержневым конструк-
циям, имеющим сложное геометрическое оформление. На основе дан-
ной технологии разработан комплекс прикладных программ, который
позволяет решать широкий класс задач научного и прикладного харак-
тера, исследовать особенности влияния различных конструктивных,
технологических и эксплуатационных факторов на температурное со-
стояние стержневых конструкций.
Работа выполнена при финансовой поддержке гранта Президен-
та РФ для государственной поддержки ведущих научных школ (про-
ект НШ–255.2012.8)
.
10


