Эффективный коэффициент теплопроводности нанокомпозита при наличии. . .
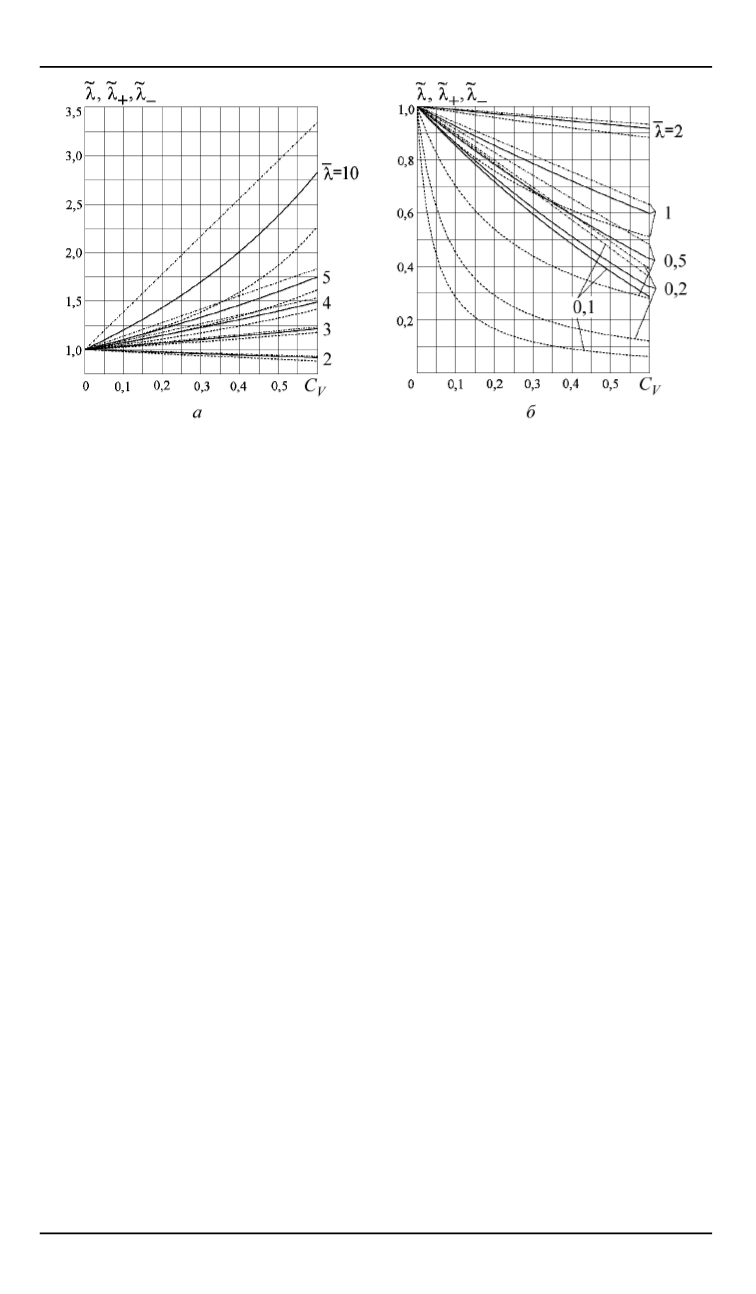
Рис. 2.
Зависимости верхней
̃︀
l
+
и нижней
̃︀
l
−
оценок отношения
̃︀
l
=
l
/
l
м
от объ-
емной концентрации при
¯
l
= 2
. . .
10
(
a
) и
¯
l
= 0
,
1
. . .
2
(
б
)
Для значений
¯
l
∈
[1
,
5]
разность
̃︀
l
+
−
̃︀
l
−
сравнительно мала и по-
этому возможную погрешность формулы (9) можно считать приемле-
мой во всем промежутке изменения объемной концентрации фуллере-
нов. Однако при
¯
l
>
5
и
¯
l
<
2
эта разность становится значительной,
особенно в случае
¯
l
<
1
(см. рис. 1,
б
и 2,
б
). Причина этого состо-
ит в использовании достаточно простых допустимых распределений
температуры и плотности теплового потока при вычислении функци-
оналов, входящих в двойственную вариационную формулировку за-
дачи теплопроводности. Можно ожидать, что построение более близ-
ких к действительным распределений позволит уменьшить разность
̃︀
l
+
−
̃︀
l
−
и тем самым точнее оценить возможную погрешность форму-
лы (9).
Работа выполнена при финансовой поддержке гранта Президен-
та РФ для государственной поддержки ведущих научных школ (про-
ект НШ–255.2012.8)
.
ЛИТЕРАТУРА
[1] Головин Н.Н., Зарубин В.С., Кувыркин Г.Н. Оценки эффективного коэффици-
ента теплопроводности композита, модифицированного фуллеренами.
Компо-
зиты и наноструктуры
, 2012, № 4, с. 15–22.
[2] Сидоров Л.Н., Макеев Ю.А. Химия фуллеренов.
Соросовский образователь-
ный журнал
, 2000, № 5, с. 21–25.
[3] Кац Е.А.
Фуллерены, углеродные нанотрубки и нанокластеры. Родословная
форм и идей
. Москва, Изд-во ЛКИ, 2008, 296 с.
[4] Поздняков В.А.
Физическое материаловедение наноструктурных материалов
.
Москва, МГИУ, 2007, 424 с.
[5] Фиалков А.С., Бавер А.И., Сидоров Н.М., Чайкун М.И., Рабинович С.М. Пи-
рографит: получение, структура, свойства.
Успехи химии
, 1965, т. 34, № 1,
с. 132–153.
7


