Г.Н. Кувыркин
Принятые допустимые распределения температуры и плотности
теплового потока для неоднородной области отличаются от действи-
тельных и поэтому значения
1
[ ]
и
1
[ ]
не будут совпадать, причем
1
[ ]
>
1
[ ]
. В промежутке между этими значениями должно быть
расположено и значение
0
= (
l
/
2)
2
0
минимизируемого функ-
ционала (10) для однородной области с коэффициентом теплопровод-
ности
l
. Тогда при
(
0
/
)
3
=
с учетом формулы (11) из условия
1
[ ]
>
0
получим
̃︀
l
6
1
−
¯
3
*
+ ¯
l
*
( ¯
3
*
−
1 + 2
b
*
) =
̃︀
l
+
,
а при использовании формулы (13) из условия
1
[ ]
6
0
найдем
̃︀
l
>
1
1
−
¯
3
*
+ ( ¯
3
*
−
1)
/
¯
l
*
+
/
(2
b
*
¯
l
*
)
=
̃︀
l
−
.
Результаты расчетов.
Для сферической оболочки в составной ша-
ровой частице положим
0
= 0
,
3899
нм и
ℎ
∘
= 0
,
075
нм, что соот-
ветствует условным параметрам фуллерена C
60
[10]. Таким образом,
в случае фуллерена
60
¯
ℎ
≈
0
,
1924
и
b
*
= 0
,
1924 ¯
l
/
¯
l
*
, где
¯
l
=
l
0
/
l
м
.
Для примера расчета примем параметр
*
= 0
,
4
, что соответствует
значению
¯
*
= 1
,
234
, и
l
*
= (
l
м
+
l
0
)
/
2
, т. е.
¯
l
*
= (1 + ¯
l
)
/
2
. В этом
случае
b
*
= 0
,
3848 ¯
l
/
(1 + ¯
l
)
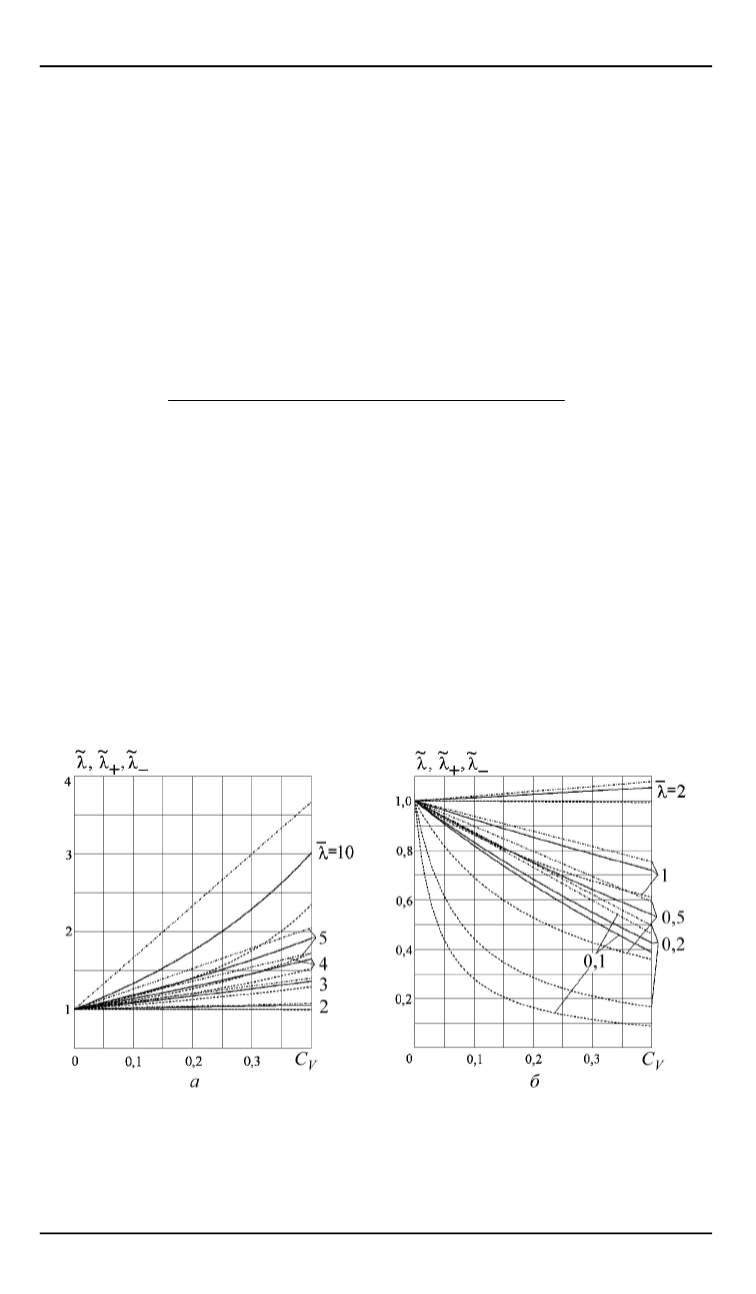
. На рис. 1,
а
,
б
при различных значениях
¯
l
приведены зависимости от объемной концентрации верхней
̃︀
l
+
и нижней
̃︀
l
−
оценок отношения
̃︀
l
=
l
/
l
м
. Сплошными линиями по-
казаны зависимости отношения
̃︀
l
от параметра , построенные по
формуле (9).
Рис. 1.
Зависимости верхней
̃︀
l
+
и нижней
̃︀
l
−
оценок отношения
̃︀
l
=
l
/
l
м
от объ-
емной концентрации при
¯
l
= 2
. . .
10
(
a
) и
¯
l
= 0
,
1
. . .
2
(
б
)
Результаты аналогичных расчетов при
*
= 0
,
6
, что соответствует
значению
¯
*
= 1
,
073
, приведены на рис. 2,
а
,
б
.
6


