Г.Н. Кувыркин
Знаменатель дроби в средней части цепочки неравенств (17) по-
ложителен. Поэтому после умножения левой части цепочки на этот
знаменатель найдем
(1
−
) + ¯
l
1
(1
−
)
2
+ ¯
l
1
(1 + ) + ¯
l
2
1
(1
−
2
)
>
>
¯
l
1
(1 + ) + ¯
l
2
1
(1
−
)
,
или эквивалентное неравенство
(1
−
¯
l
1
)
2
(1
−
)
>
0
. Знамена-
тель правой части цепочки неравенств (17) также положителен, что
после умножения средней части цепочки на этот знаменатель и умно-
жения правой части на положительный знаменатель дроби в соотно-
шении (17) позволяет записать
¯
l
1
(1
−
+ ¯
l
1
)
(︀
1 + + ¯
l
1
(1
−
)
)︀
>
¯
l
1
(︀
1
−
+ ¯
l
1
(1 + )
)︀
.
Это неравенство эквивалентно неравенству
¯
l
1
(1
−
¯
l
1
)
2
(1
−
)
>
0
.
Параметрический анализ.
Прежде всего проведем сравнение
значений параметров
∘
a
, определяемых при ожидаемых значениях
¯
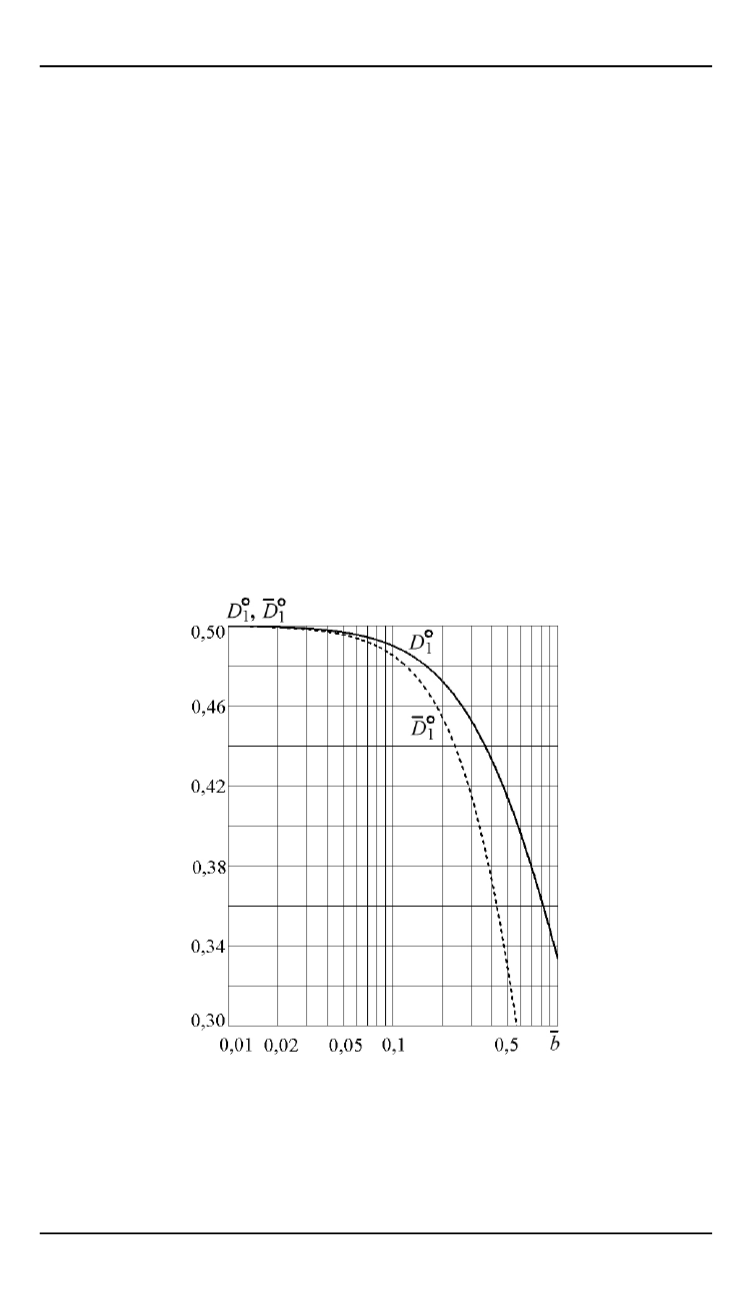
соотношениями (3) и (4). На рис. 1 в полулогарифимических коорди-
натах представлены зависимости параметров
∘
1
и
¯
∘
1
от значения
¯
,
определяемые первыми формулами (3) и (4) соответственно.
Рис. 1.
Зависимости параметров
∘
1
и
¯
∘
1
от значения
¯
Ясно, что уже при
¯
<
0
,
1
различие пренебрежимо мало. При
¯
<
0
,
01
с точностью
0
,
0003
из обеих формул следует
∘
1
= ¯
∘
1
= 1
/
2
.
Таким образом, использование предельных значений
¯
∘
a
обеспечивает
достаточную точность для практических приложений.
6


