A.O. Шишанин
8
2
1 1
1 1 1
1
(0)
;
( 1)
.
1 log
1
1 2 log
1
q
q
q q
q
q
q
q
В классическом пределе
q
→ 1 получены формулы Эйлера (2):
1
1
1
1
lim (0)
; lim ( 1)
.
2
12
q
q
q
q
В общем случае
1
1
lim ( )
.
1
m
q q
B m
m
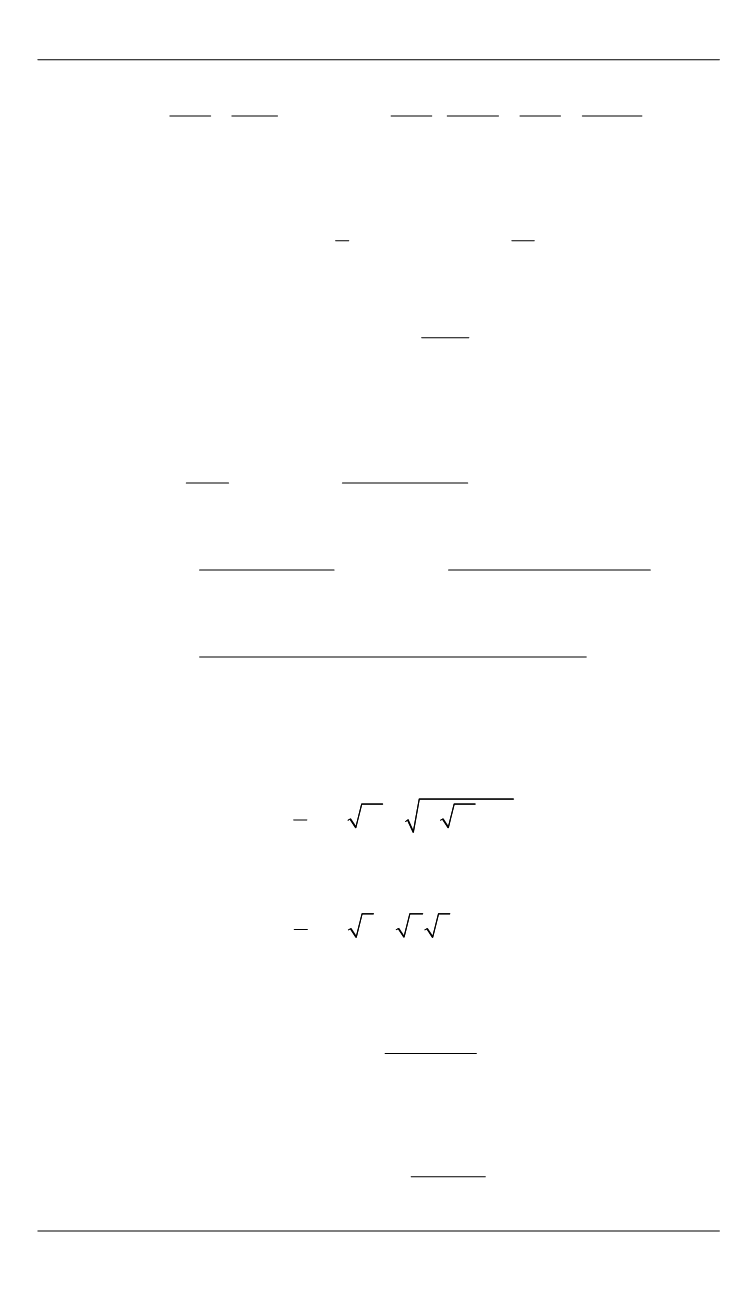
Рассмотрим знакопеременный случай, когда формула (4) прини-
мает следующий вид в неположительных целых точках:
2
4 3 2
3
2
4
3
2
2
4
3
4 3 2
4
3
2
1
(0)
;
( 1)
;
1
(
1)( 1)
( 1)
(
1)
( 2)
;
( 3)
;
(
1)(
1)
(
1)(
1)(
1)
( 1)(
1)(
2 2 1)
( 4)
.
(
1)(
1)(
1)(
1)
q
q
q
q
q
q
q
q q
q q
q q q q q
q q
q q q
q q q q q q q
q q q q q q q
(5)
Полученные формулы (5) переходят в классические формулы
Эйлера (3). Действительными нулями ( 3)
q
являются
q
1
= 0 и
2,3
1 (1 13 2( 13 1),
4
q
а нули ( 4)
q
суть 0, 1 и
4
1 (1 3 2 3).
2
В свою очередь,
q
-аналог дзета-функции Гурвица задается рядом
(
)( 1)
0
( ; )
.
[
]
n a s
s
n
q
s a
n a
В классическом пределе
q
→ 1 для натуральных
m
можно получить
1
1
( )
lim ( ; )
.
1
m
q q
B a
m a
m


