А.А. Федотов, П.В. Храпов
2
где
,
0, 1, ...,
i
x i
n
и
1
,
1, 2, ...,
i
i
i
h x x i
n
— узловые точки и
шаги сетки соответственно.
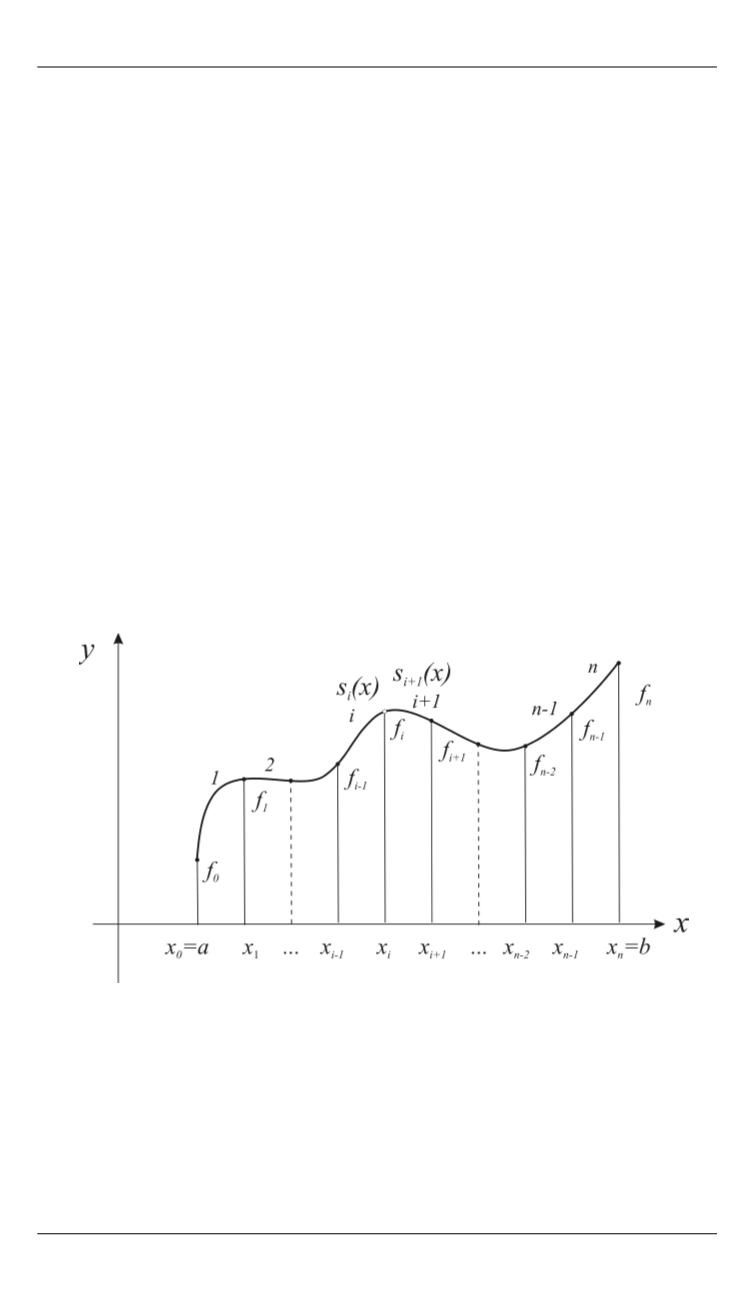
Требуется по известным значениям
( ),
0, 1,...,
i
i
f
f x i
n
по-
строить на отрезке [ , ]
a b
функцию ( ),
S x
достаточно близкую к
( ).
f x
Функцию ( )
f x
принято называть
интерполируемой
, ( )
S x
—
интерполирующей функцией
, а точки
i
x
—
узлами интерполяции
.
Поставленную в общей форме задачу о приближении функций бу-
дем решать с помощью интерполяционного кубического сплайна [1–4].
Построение интерполяционного кубического сплайна.
Назо-
вем отрезок
1
[ , ],
1, 2, ..., ,
i
i
x x i
n
i-м частичным
отрезком
.
Интерполяционным кубическим сплайном
для функции
( )
f x
называется функция
( ),
s x
удовлетворяющая следующим условиям:
1) на каждом частичном отрезке
1
[ , ],
1, 2, ...,
i
i
x x i
n
функция
( )
s x
является многочленом третьей степени;
2) ( ), ( )
s x s x
и ( )
s x
являются непрерывными функциями на от-
резке [ , ]
a b
;
3) выполнены условия интерполирования:
( )
,
0, 1, ...,
i
i
s x f i
n
(рисунок).
Интерполирование функции
( )
f x
На каждом из частичных отрезков
1
[ , ]
i
i
x x
сплайн будем искать
в виде
2
3
1
1
1
( )
(
)
(
)
(
) ,
i
i
i
i
i
i
i
i
s x a b x x c x x
d x x
(2)
1
[ , ],
1, 2,..., .
i
i
x x x i
n


