Определение динамических характеристик гранулированных сред. . .
Для второго образца толщиной слоя
ℎ
= 0
,
56
см после анало-
гичных исследований определено значение
r
2
= (1
,
72
±
0
,
14)
г/см
3
.
Сравнение этих данных с результатами, полученными резонансным
методом для резонатора с жесткими стенками, приводит по четырем
замерам к значениям
r
в диапазоне
1
,
6
. . .
2
,
0
г/см
3
, а среднее значение
и среднеквадратическое отклонение равны
r
=(1
,
75
±
0
,
15)
г/см
3
.
Полученные результаты убедительно свидетельствуют о зависи-
мости динамической плотности гранулированной среды, заполненной
жидкостью, от частоты акустического воздействия. Физическое объяс-
нение этой зависимости заключается в уменьшении толщины погра-
ничного слоя жидкости, окружающей гранулы (песчинки), при увели-
чении частоты. Данное обстоятельство приводит к эффекту независи-
мости колебаний жидкости и гранул среды. Следуя электромеханиче-
ской аналогии, запишем выражение для
r
(
w
)
при
w
→ ∞
:
r
(
∞
) =
[︂
1
(1
−
h
)
r
*
+
1
hr
0
]︂
−
1
,
где
r
*
= 2
,
75
г/см
3
,
r
0
= 1
г/см
3
.
Определение скорости звука.
При некоторой модификации экс-
периментальной установки возможно определение скорости звука в гра-
нулированной среде, пропитанной несжимаемой жидкостью, без замены
акустически мягкого дна сосуда на жесткое. Пусть слой образца в со-
суде размерами
× ×
ℎ
размещается на произвольной высоте
0
,
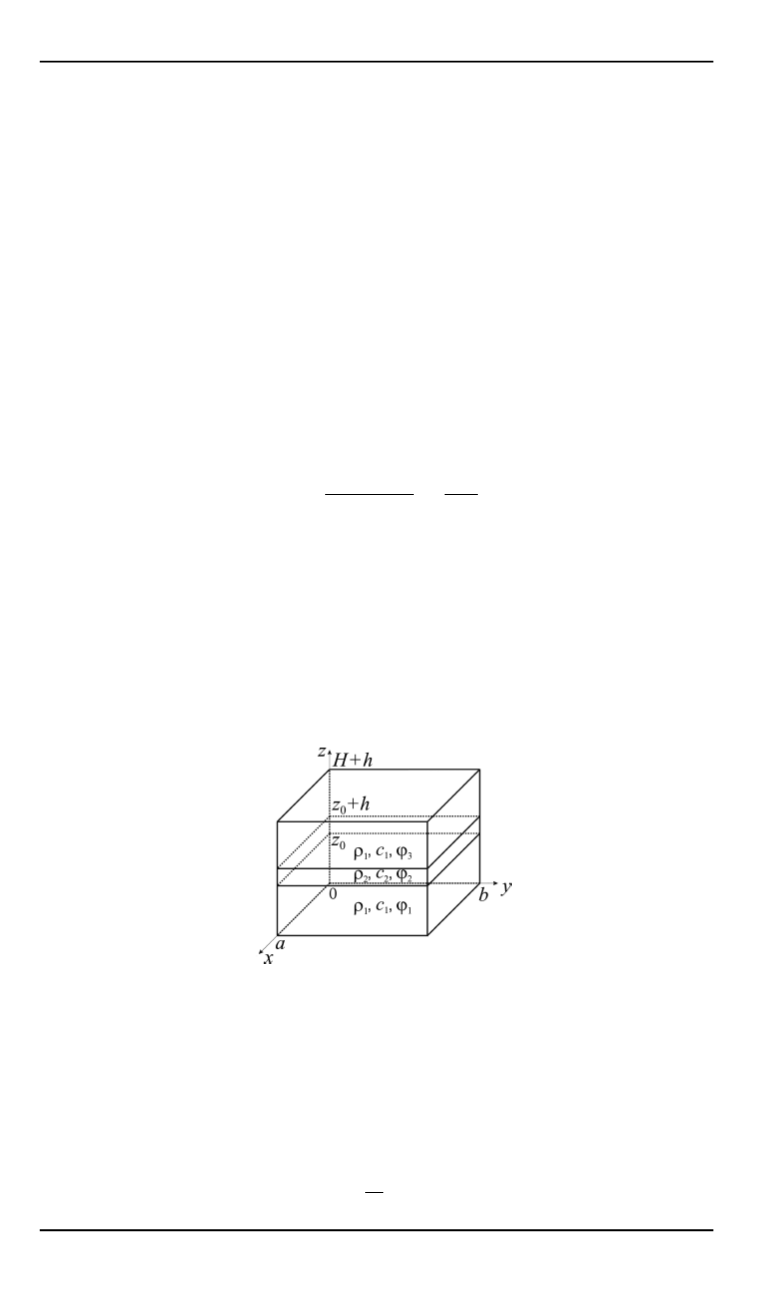
например слой подвешен на сетке из тонкой проволоки (рис. 3).
Рис. 3.
Слой образца среды, расположенный на высоте
0
В рамках предыдущих ограничений и сохраняя прежние обозначе-
ния (
r
1
,
1
— плотность и скорость звука в жидкости,
r
2
,
2
— в образце
среды), введем звуковой потенциал
3
1
в слое жидкости под слоем гра-
нулированной среды,
3
2
— в образце,
3
3
— в слое жидкости над слоем
образца. Тогда можно сформулировать следующую краевую задачу
D3
+
2
3
= 0
,
=
˜
w
,
= 1
,
2
,
3
,
= 1
,
2
,
(11)
7


