В.П. Строгалев, И.О. Толкачева
8
Аналогично для случая атаки вдоль поперечной оси имеем
P
2
= 0,378;
M
2
= 2,27.
Для реализации метода Монте-Карло была написана программа,
осуществляющая розыгрыш по нормальному закону точек попадания
ракет в контур цели, расположенной под произвольным углом к направ-
лению стрельбы. Координаты точек попадания рассчитывались по сле-
дующим формулам:
X
= μ
x
+
N
(0,1)σ
x
,
Y
= μ
y
+
N
(0,1)σ
y
.
Здесь μ
x
= μ
y
= 0;
N
(0,1) — нормально распределенное случайное число
с нулевым математическим ожиданием и единичным среднеквадрати-
ческим отклонением.
Далее подсчитывается количество попаданий в прямоугольник со
сторонами
а
и
b
, ориентированный под различными углами относи-
тельно направлений рассеивания (угол изменяется в диапазоне 0…180º).
Для каждого из задаваемых, изменяющихся с шагом в 1º углов ориен-
тирования прямоугольника, проводится по
N
реализаций метода, для по-
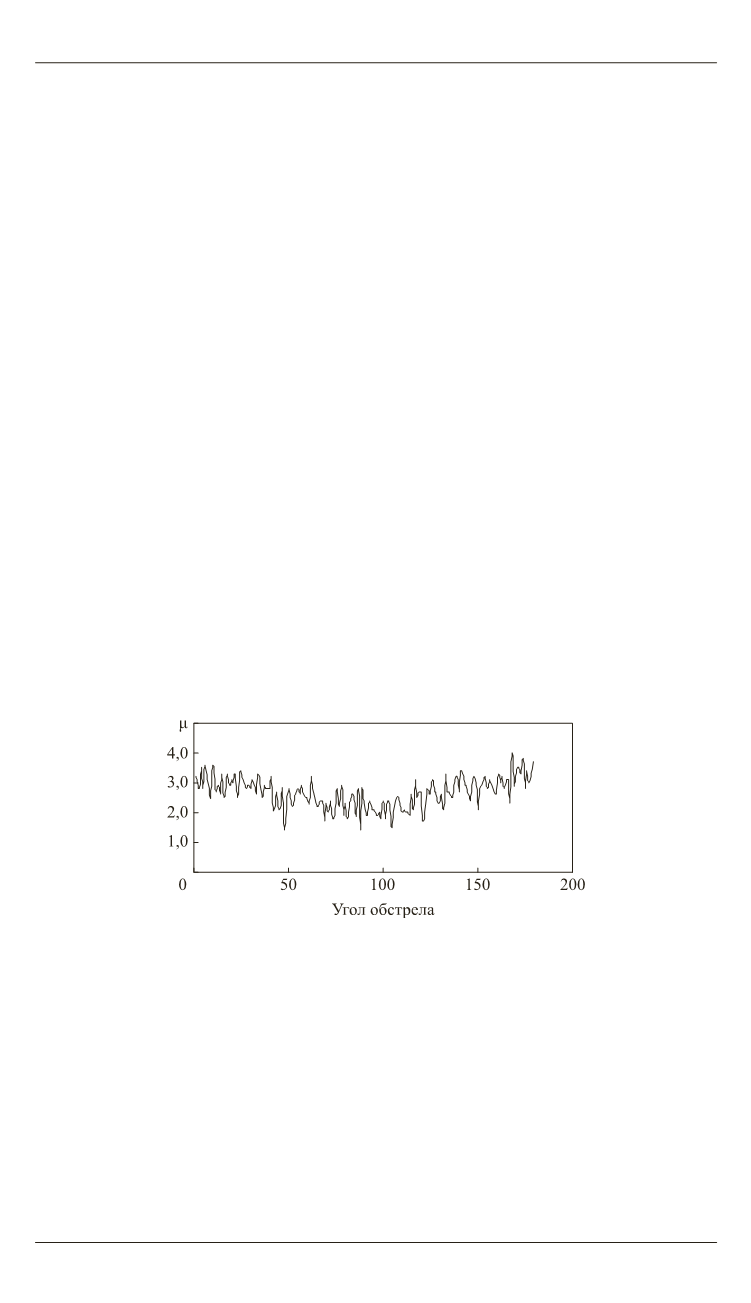
иска среднего числа попаданий μ в цель. Зависимость среднего числа
попаданий от угла обстрела цели приведена на рис. 2.
Рис. 2.
Зависимость среднего числа попаданий от угла обстрела
Из полученной картины обстрела площадной цели очевидно, что
при заданных вероятностных параметрах атаки и геометрических разме-
рах цели наиболее эффективной является атака, предпринимаемая в на-
правлении, совпадающем с направлением продольной оси цели, а наи-
менее эффективной — в направлении, совпадающем с поперечной осью.
Результаты, полученные с использованием метода Монте-Карло при
сравнительно небольшом количестве его реализаций (
n
= 10), с высокой


