Решение прикладных технических задач методом имитационного моделирования
7
Для расстояния, с которого запускаются ракеты, оба отклонения
независимы, нормально распределены относительно точки прицелива-
ния и имеют нулевое среднее значение. Среднеквадратические откло-
нения, м: по дальности σ
x
= 60 и боковому направлению σ
y
= 120.
При каждом заходе бомбардировщик выпускает шесть ракет (
n
= 6).
Необходимо оценить среднее число попаданий при каждой атаке.
В данном случае возможны несколько вариантов захода на атаку
бомбардировщика, связанных с взаимным расположением предприятия
и атакующего самолета. При этом задача может быть решена аналити-
ческим методом (с использованием таблиц функций Лапласа) и методом
Монте-Карло. Для случаев заходов на атаку самолета с направлений,
совпадающих с направлениями продольной или поперечной осей сим-
метрии предприятия, решение легко получить аналитически, тогда как
для остальных случаев такое решение получается громоздким, и ана-
литический подход себя не оправдывает. Методом Монте-Карло задача
может быть решена для любого направления захода на атаку с практи-
чески одинаковыми трудозатратами, что является в данном случае оче-
видным преимуществом метода, а аналитический подход может ис-
пользоваться для проверки результатов частных случаев реализации
метода Монте-Карло.
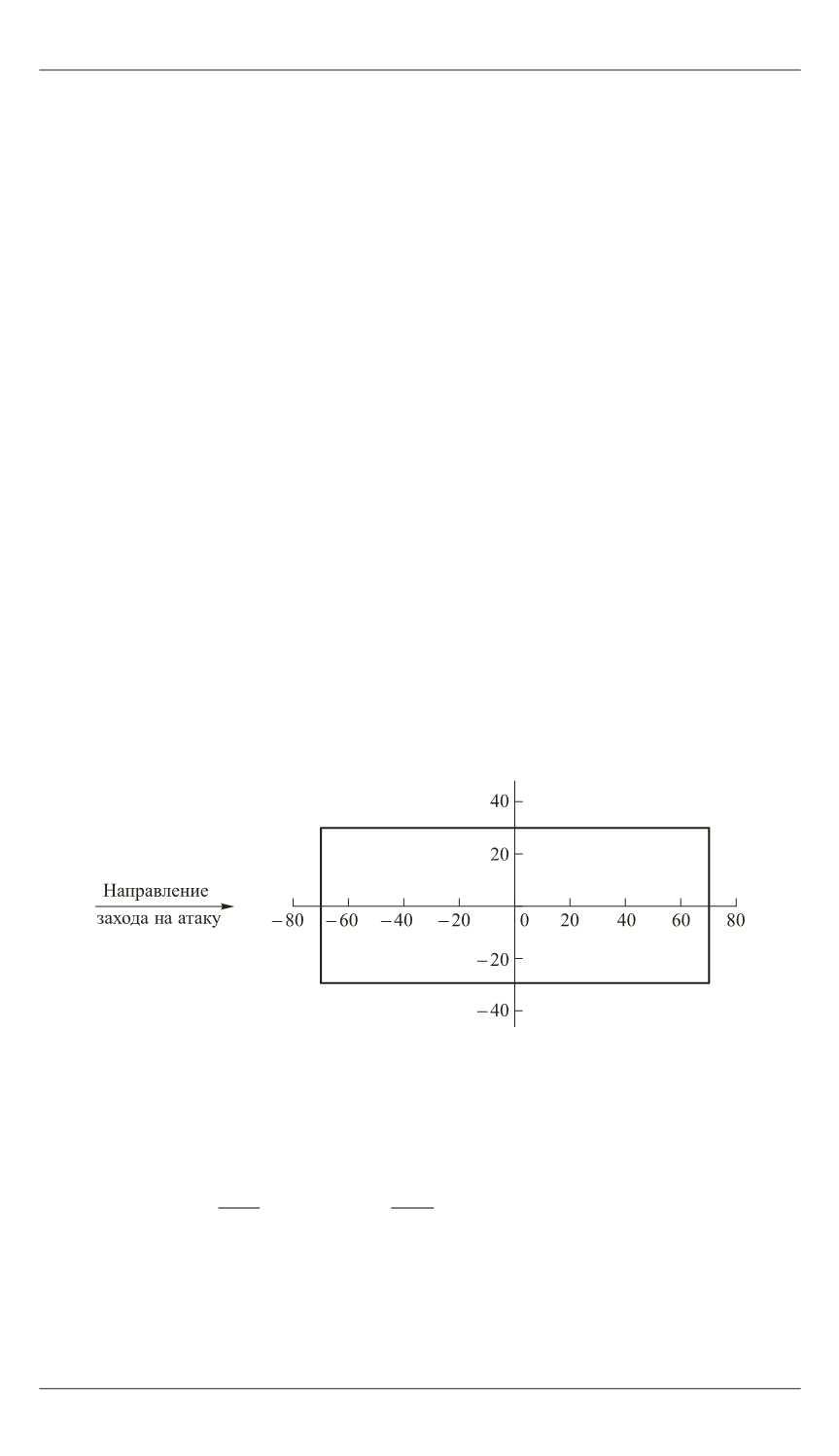
Рассмотрим в первую очередь теоретическое решение для случая
захода самолета на атаку вдоль продольного направления (рис. 1).
Рис. 1.
Схема бомбардировки промышленного объекта
Используя формулы [3] для определения вероятности попадания
в площадь цели, имеем
1
0
0
2
1 2
1 0,788 0,682 0,538,
2
2
x
y
a
b
P F
F
=
−
− = ⋅
=
σ
σ
где
F
0
— стандартная функция нормального распределения.
Тогда среднее число попаданий за одну атаку
M
1
=
nP
1
= 6 ∙ 0,538 = 3,23.


