Обзор и анализ исследований тепломассообмена в стратифицированной морской воде
15
мальной плотности
( , ).
m
s p
Именно это условие использовали в ра-
ботах [30, 31, 34, 40], но при
0
s
и
q
= 2. Согласно уравнению
(26), должно выполняться условие
0
( )
( ).
m
d x t
t
t
t
f x
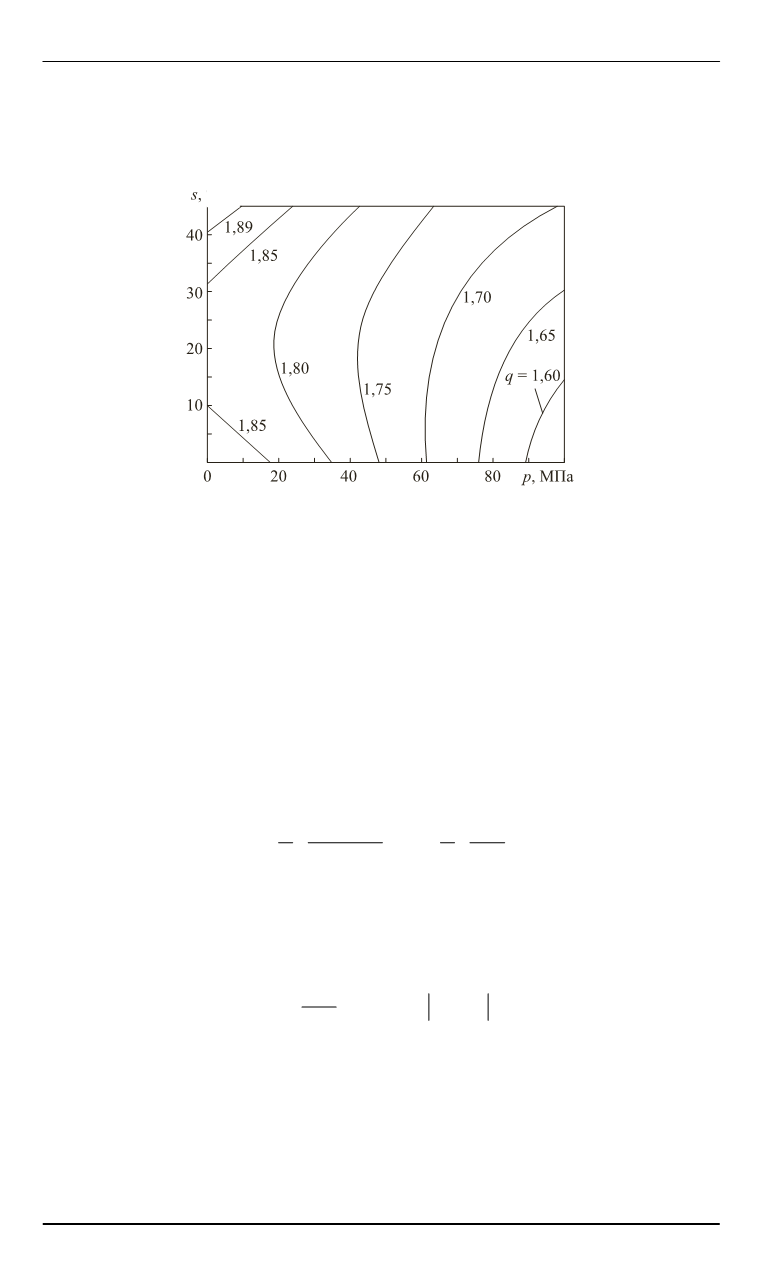
Рис. 4. Линии постоянных значений
q
в зависимости от солености и
давления [25]
Принимая
m
t
в качестве характерной температуры (например,
r
t
в соотношении (18)) и предполагая на время, что имеется стратифи-
кация по температуре в направлении диффузии, получаем условие,
что
0
t
и
t
не должны зависеть от
х
. В таком случае
R
= const.
Анализируя выражения для
С
1
и
С
2
можно показать, что
b
и
с
должны изменяться в зависимости от
х
либо по степенному, либо по
экспоненциальному закону. Если при
n
= 0 принять
С
1
= 3,
С
2
= –1,
С
3
= 1 и
С
4
= 0, то для
b
(
х
) получаем выражение
1/4
1/4
3
2
2
1
1 Gr
( )
,
4
4
q
x
g x d
b x
x v
x v
(29)
которое близко к соотношению, характеризующему приближение
Буссинеска, за исключением того, что теперь число Грасгофа
3
0
2
Gr
( , )
.
4
q
x
gx s p t t
v
(30)
Однако, как указано в работе [26], функция
( )
b x
всегда положи-
тельная, хотя выталкивающая сила может быть положительной, от-
рицательной или знакопеременной в зависимости от соотношений
между
0
t
и
,
m
t
а также
t
и
.
m
t
Этот недостаток можно устранить,
если использовать число Грасгофа
Gr
x
вида (20). Пусть
—
‰


