
Оптимизация экспедиции к Фобосу космических аппаратов с комбинированной тягой…
Инженерный журнал: наука и инновации
# 7·2017 5
Формализация.
В связи с потерей точности [16], связанной с
тем, что при использовании какой-либо одной системы координат
(СК) вычисление правых частей дифференциальных уравнений дви-
жения КА вблизи Земли или вблизи Марса имеет значительные по-
грешности вследствие вычитания близких значений координат КА и
притягивающего центра. Движение КА на каждом из пяти участков
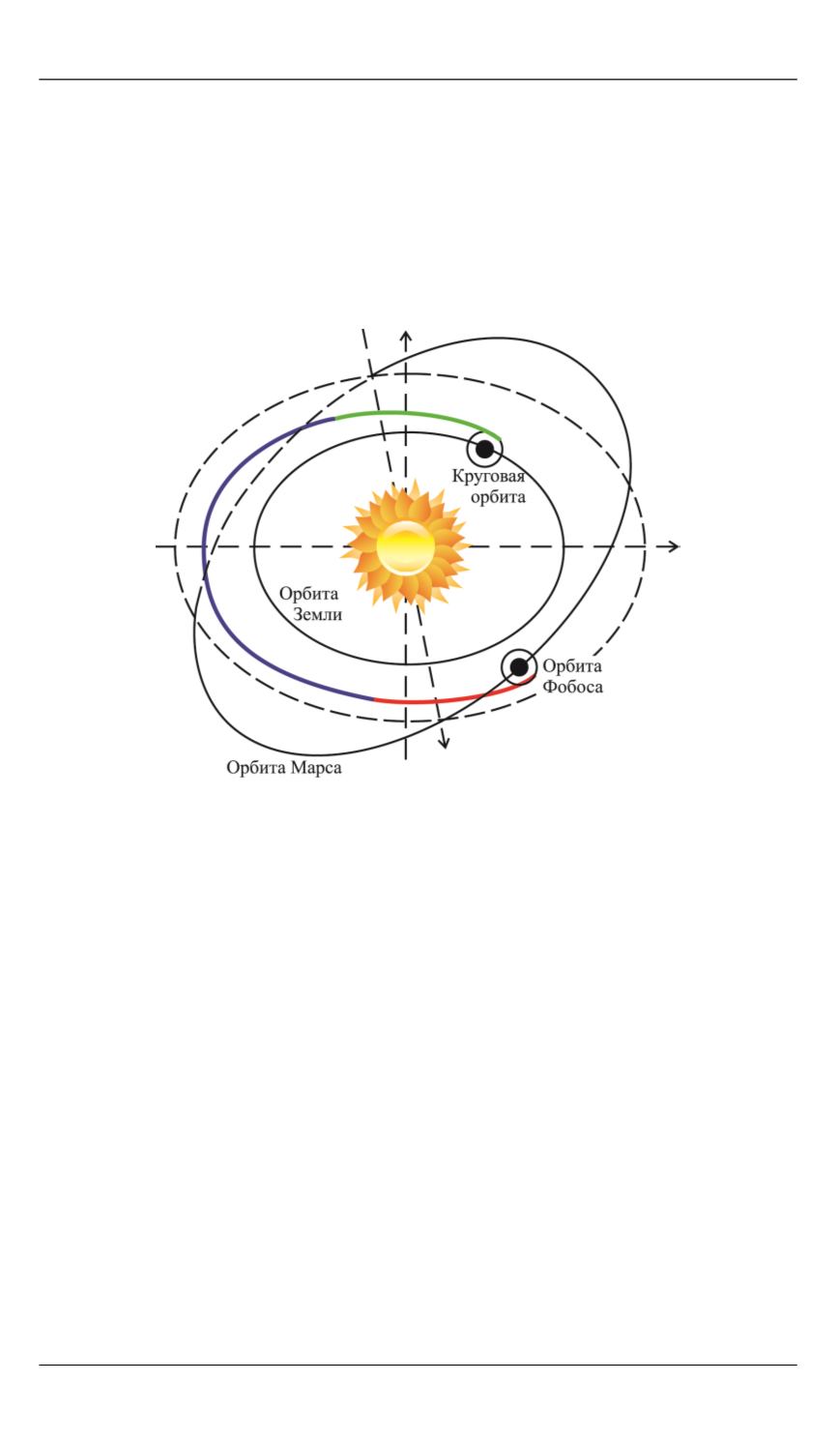
траектории рассматривается в одной из трех различных СК (рис. 1).
Рис. 1.
Схема перелета от Земли к Марсу
На схеме (см. рис. 1) первой части экспедиции зеленым цветом
выделен участок использования геоцентрической СК, синим — ге-
лиоцентрической и красным (при подлете к Марсу) — марсоцентри-
ческой. Задача возвращения рассматривается сначала в марсоцентри-
ческой, а затем в гелиоцентрической СК. Причем эти СК — невра-
щающиеся декартовы, их оси параллельны осям СК J2000. Ниже во
всех формулах
i
= 1…5 — номер участка траектории.
Отметим, что на 1-м, 3-м и 4-м участках СК являются неинер-
циальными.
Данная задача космодинамики как задача оптимального управле-
ния формализуется совокупностью динамических систем, поскольку
вид дифференциальных связей изменяется в зависимости от участков
траектории вследствие разных СК, и решается на основе соответ-
ствующего принципа максимума [17].
На каждом из пяти участков траектории компоненты векторов
положения и скорости КА обозначим
,
i
x
,
i
y
i
z
и
, ,
i i
i
u v w
соответ-
















