
Г.Г. Плавник, А.Н. Лошкарев, О.Л. Точилова
4
Инженерный журнал: наука и инновации
# 9·2016
для некоторого ограниченного числа выбранных вариантов сочета-
ния допусков. Их выбор чаще всего основан на детерминированном
подходе, при котором анализ проводится не только для номинальных
характеристик (режим
N
), но и еще для двух вариантов сочетания до-
пусков, приводящих соответственно к повышению устойчивости
(режим
N
+) и к ее понижению (режим
N
–).
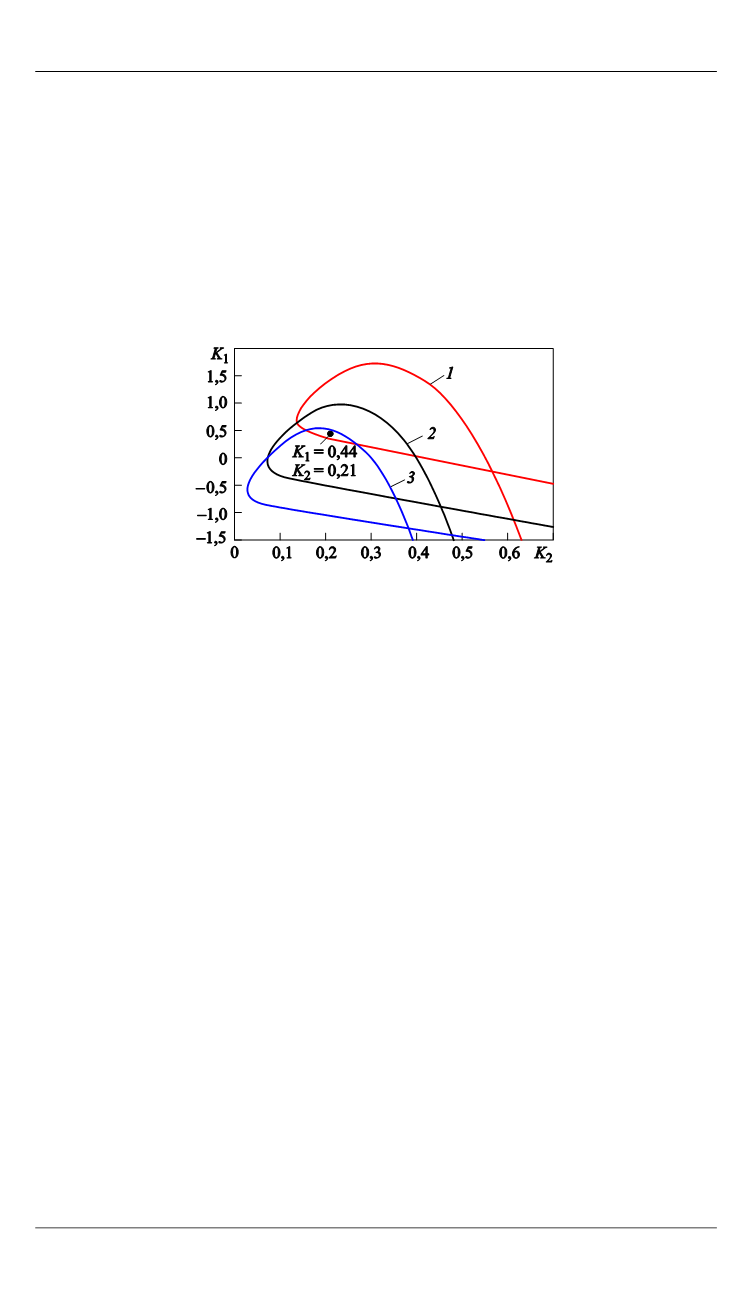
На рис. 3 представлен один из вариантов расположения областей
устойчивости для режимов
N
,
N
+,
N
– и указаны значения коэффици-
ентов стабилизации, выбранные в зоне пересечения этих областей.
Рис. 3.
Пример расположения областей
устойчивости для режимов
N
– (
1
),
N
(
2
),
N
+ (
3
) в плоскости коэффициентов стаби-
лизации
K
1
и
K
2
При таком подходе полученные коэффициенты стабилизации
ориентированы на наиболее неблагоприятные сочетания предельных
возмущений характеристик БПЛА, что в ряде случаев приводит
к значительному ухудшению качества управления в номинальных
условиях. Кроме того, при большом числе допусков их влияние на
различных траекториях становится неочевидным и число критиче-
ских вариантов сочетания допусков не исчерпывается двумя режи-
мами
N
+ и
N
–.
В силу того что разбросы характеристик БПЛА имеют случайную
природу, подчиняясь тому или иному закону вероятностного распре-
деления, анализ работы алгоритма стабилизации основан на исполь-
зовании статистического моделирования движения БПЛА в ЦМК для
большого числа случайно реализовавшихся наборов допусков (по-
рядка 1000 и более), каждому из которых соответствует свой пере-
ходный процесс.
В этом случае логично было бы проводить корректировку коэф-
фициентов стабилизации по результатам частотно-временного анали-
за полученных при статистическом моделировании переходных про-
цессов (порядка 1000 и более), так как указанный подход позволил
бы обеспечить необходимое качество управления с учетом малой


















