
Г.Г. Плавник, А.Н. Лошкарев, О.Л. Точилова
2
Инженерный журнал: наука и инновации
# 9·2016
является нелинейной, вследствие чего реальные области устойчиво-
сти могут быть сдвинуты относительно линейных областей или
иметь другие размеры и форму. Таким образом, линейные области
могут дать только начальное приближение для значений коэффици-
ентов стабилизации, последующая корректировка которых представ-
ляет собой отдельную достаточно трудоемкую задачу. Кроме того,
в силу сложности объекта управления приемлемость выбранных ко-
эффициентов стабилизации может быть определена только в резуль-
тате анализа качества переходных процессов, полученных при моде-
лировании движения БПЛА с использованием цифрового моделиру-
ющего комплекса (ЦМК).
Постановка задачи.
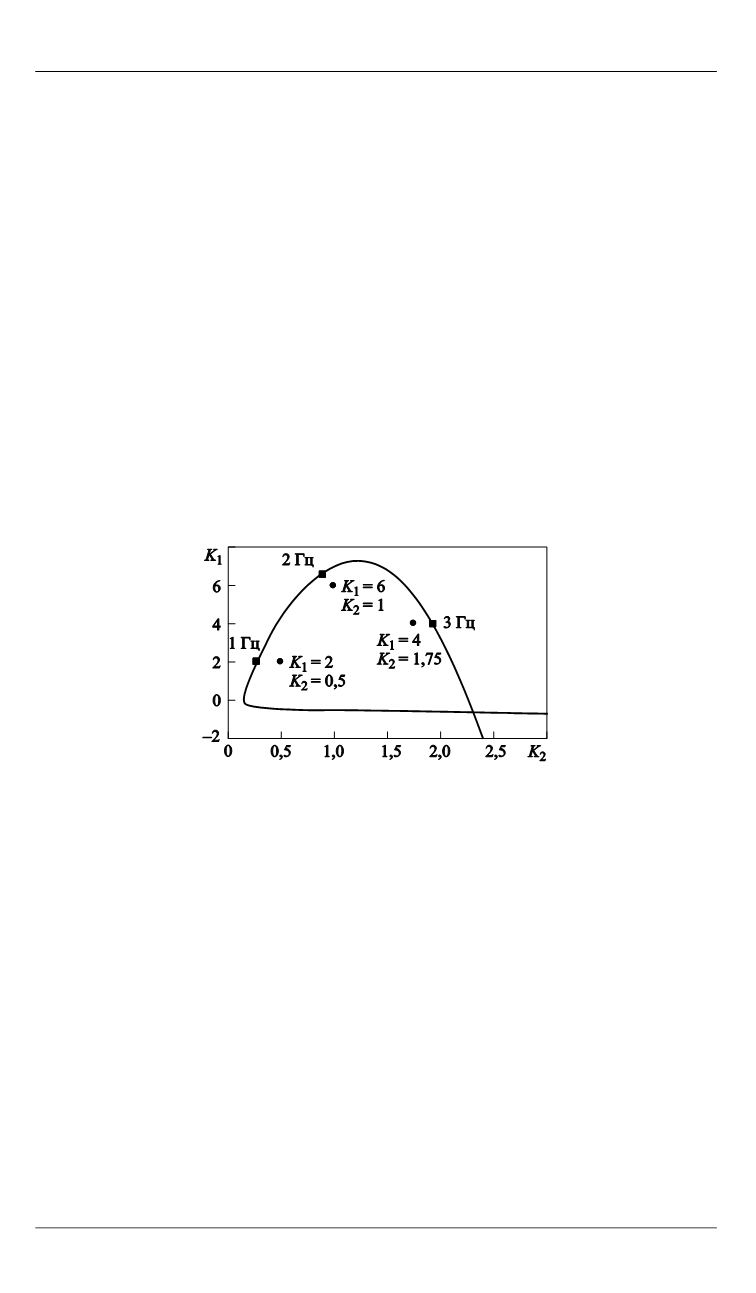
На рис. 1 приведен пример области устой-
чивости в плоскости коэффициентов стабилизации
1
K
и
2
K
для ли-
нейной математической модели движения БПЛА, а на рис. 2 — вид
переходных процессов в зависимости от расположения
1
K
и
2
K
в этой области [2].
Рис. 1.
Область устойчивости в плоскости
коэффициентов стабилизации
K
1
и
K
2
При сравнении рис. 1 и 2 видно, что при приближении
1
K
и
2
K
к какой-либо из границ области в переходном процессе сильнее про-
является частота, соответствующая этой границе. Отсюда следует,
что по спектральному составу переходных процессов можно оценить
положение коэффициентов стабилизации в области устойчивости,
а также при необходимости скорректировать их значения в соответ-
ствии с полученными оценками.
Рассмотренная взаимосвязь положения коэффициентов стабилиза-
ции в областях устойчивости и характеристик переходных процессов
справедлива и в случае изменения областей устойчивости вследствие
нелинейностей в предположении, что все нелинейности, присутству-
ющие в модели объекта управления, не приводят к структурной не-
устойчивости.


















